网络流学习笔记
更正了文章的远古问题,具体的就是 Dinic 全部写的 EK(很唐)。
定义
网络
网络是一个由 个点 条边组成的有向图 ,满足每一条边 都有边权 ,我们称 为容量。图中还有两个特别的点,分别是源点 和汇点 ,满足 。
流
如果函数 满足以下的要求,那么我们称函数 为流函数。
- 容量限制:对于任意边 ,满足 。
- 斜对称:对于任意边 ,满足 。
- 流量守恒:对于所有的边 和 ,满足其函数 的和相等。
对于任意边 ,其 称为变得流量, 称为边的剩余流量。对于所有的边 的 的和被称为这个网络的流量。定义所有的剩余流量不为 的边组成的网络为残量网络。
总结
通俗的理解,网络就是一个很理想的自来水供应系统,每一个管道都有自己的单位时间内的最大流量。即使在前面给出的水再多一旦超出了容量,这根管道也只能运送容量之内的。在这个自来水系统中有一个超级无敌牛逼的无限出水水库被称为源点和一个无限吃水的超级无敌牛逼小区被称为汇点。
这个自来水系统满足管道的中间不会有水的残留或者溢出,而且在流动的过程中并不会有新的水加入,并且水库与小区并不在一起。其中,容量指单位时间最多可以通过的水,流量表示单位时间实际流过的水,剩余容量表示容量减去流量也就是浪费的流量。
最大流
定义
给定一个网络,最大流就是求出在这个网络的所有流中流量最大的流。
Frod-Fulkerson
增广路
如果一个路径满足以下要求,那么它就是一个增广路:
- 其起点与终点分别是源点 和汇点 。
- 对于这个路径中所有边 的流量剩余容量 。
求解方法
对于一种暴力的方法,我们可以一直寻找增广路知道寻找不到为止。在找到一条增广路之后,计算出路径上剩余容量的最小值 。接着将路径上所有的剩余容量减少 再将网络的总流量也就是答案增加 就好了。
但是有一个问题,这样在某些情况下只能找到一些较优解:
显而易见的,如果使用 和 可以得到的流是 。
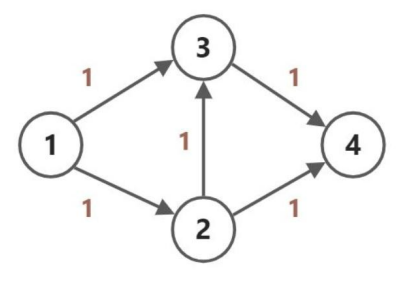
可是在使用直接 dfs 进行搜索之后,可能会得到一个为 的路径,这样得到的流就只有 了。
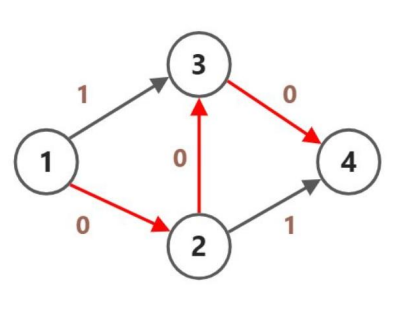
为了解决这个问题,我们可以考虑一种类似反悔贪心的手段避免上面情况发生。在每一次找到增广路时,在将这面走的剩余流量减少 的时候,同时将增广路的反边的剩余流量增加 。
同样是上面的问题,在建出给定的网络之后我们又为每一条边建一个反边:
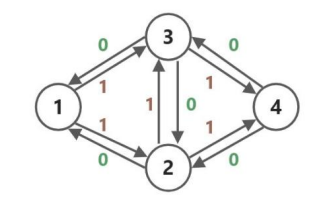
接着,在直接 dfs 得到一条增广路 之后,将原有的边与反边全部更新得到下图:
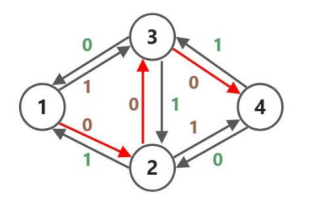
继续寻找新的增广路,得到 。
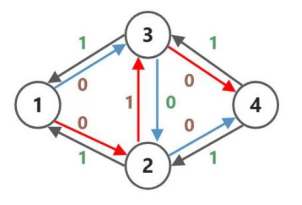
因为两次遍历及经过了 也经历的 所以它们的贡献就被抵消了,其效果与直接进行 是一样的。
在使用 dfs 不断寻找增广路知道不存在是,Frod-Fulkerson 算法就完成了,这个网络的最大流就是增广路的贡献。
假设流量为 ,那么其时间复杂度在最坏情况下为 ,因为可能每一次增广路得到的 都是 。
实现
bool bfs(int rGraph[V][V], int s, int t, int parent[])
{
bool visited[V];
memset(visited, 0, sizeof(visited))
queue<int> q;
q.push(s);
visited[s] = true;
parent[s] = -1;
// Standard BFS Loop
int u;
while (!q.empty())
{
// edge: u -> v
u = q.front(); // head point u
q.pop();
for (int v = 0; v < V; ++v) // tail point v
{
if (!visited[v] && rGraph[u][v] > 0) // find one linked vertex
{
q.push(v);
parent[v] = u; // find pre point
visited[v] = true;
}
}
}
return visited[t] == true;
}
int fordFulkerson(int graph[V][V], int s, int t)
{
int u, v,rGraph[V][V];
for (u = 0; u < V; ++u)
{
for (v = 0; v < V; ++v)
{
rGraph[u][v] = graph[u][v];
}
}
int parent[V],max_flow = 0;
while (bfs(rGraph, s, t, parent))
{
// edge: u -> v
int path_flow = INT_MAX;
for (v = t; v != s; v = parent[v])
{
// find the minimum flow
u = parent[v];
path_flow = min(path_flow, rGraph[u][v]);
}
// update residual capacities of the edges and reverse edges along the path
for (v = t; v != s; v = parent[v])
{
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow; // assuming v->u weight is add path_flow
}
max_flow += path_flow;
}
return max_flow;
}
Edmonds-Karp
求解方法
简单的说,Edmonds-Karp 就是在 Frod-Fulkerson 的基础上,将栈改为了队列,或者说将 dfs 实现改为了 bfs 实现。虽然其表面上只是更改了实现方式,但是这也是为 Frod-Fulkerson 添加了一个优化:每次增广最短的增广路。这个优化其实很重要,因为在优化之后其最劣复杂度就被控制在了 。
时间复杂度证明
在找到一条增广路之后,我们可定需要将可以压榨的全部榨干,也就是肯定有一条边被跑慢,我们定义这一条边为关键边。所以经过增广操作,这些边因为剩余流量为 所以在残余网络中就被无视掉了,也就是这一条增广路就断开了。所以我们每一次进行增广操作,其实就是破坏增广路。所以从 到 自然就会单调递增,也就保证了 bfs 搜索的正确性。
因为每一次将一条增广路破坏之后都至少有 条边被从残量网络中被删除,所以求解增广次数就可以与关键边的出现次数进行直接的联系。
因为关键边会从残量网络中消失,直到反向边上有了流量才会恢复成为关键边的可能性,而当反向边上有流量时最短路长度一定会增加。显而易见,增广路的长度肯定位于 到 之间,所以总共的增广次数为 次。
因为在 Edmonds-Karp 中计算残量网络的方法为 bfs 其时间复杂度为 ,所以总共的时间复杂度就应该为 。
实现
int Bfs() {
memset(pre, -1, sizeof(pre));
for(int i = 1 ; i <= n ; ++ i) flow[i] = INF;
queue <int> q;
pre[S] = 0, q.push(S);
while(!q.empty()) {
int op = q.front(); q.pop();
for(int i = 1 ; i <= n ; ++ i) {
if(i==S||pre[i]!=-1||c[op][i]==0) continue;
pre[i] = op; //找到未遍历过的点
flow[i] = min(flow[op], c[op][i]); // 更新路径上的最小值
q.push(i);
}
}
if(flow[T]==INF) return -1;
return flow[T];
}
int Solve() {
int ans = 0;
while(true) {
int k = Bfs();
if(k==-1) break;
ans += k;
int nw = T;
while(nw!=S) {//更新残余网络
c[pre[nw]][nw] -= k, c[nw][pre[nw]] += k;
nw = pre[nw];
}
}
return ans;
}
总结
虽然比起 Frod-Fulkerson 来说 Edmonds-Karp 已经优秀了许多,但是因为 一般为 级别,所以这个算法的之间复杂度其实是可以达到 的级别,这依旧很难接受。
经过分析容易发现,在 Edmonds-Karp 求解了一次增广路之后它都要重新计算一次残量网络,十分耗费时间。如果可以将在一个网络中所有的增广矩阵在一次中全部求解出来在再进行增广操作,那么效果可能就会得到一个优化。
Dinic
分层图
我们可以定义一个叫分层图的概念:如果 到 的距离为 ,那么点 位于第 层。
理论上的求解方法
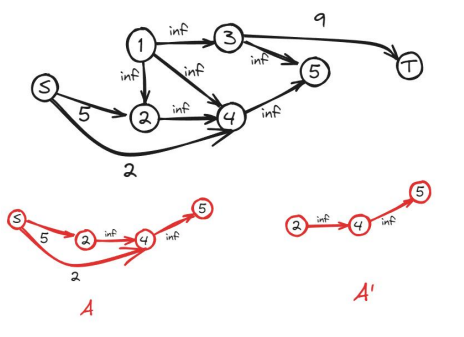
对于下方的这个网络,在所有边的边权均为 的情况下先跑一个最短路。
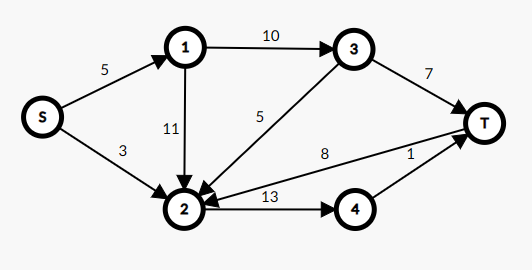
可以得到 ,,,。所以我们就把 分到第 层, 分到第 层, 分到第 层, 单独分到第 层。
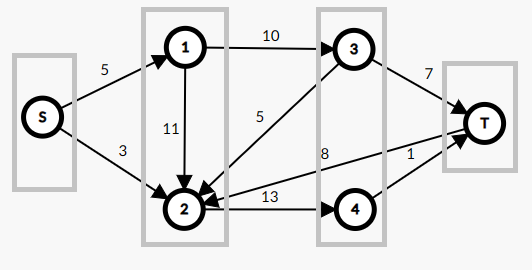
因为反向边都不在最短路上,所以我们可以将他们忽视。同时在一层中的路线对于最短路也是没有贡献的,所以将他们也删除。通过这些优化,得到下面的一张图。
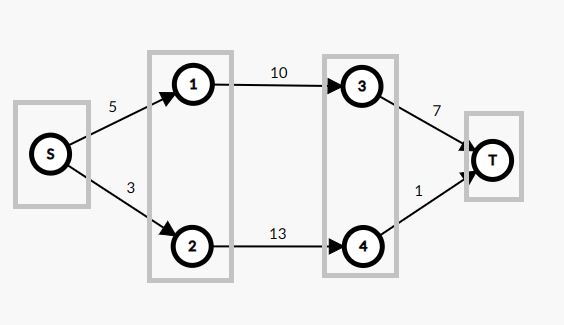
在分层结束之后,所有的剩余流量非 的边都在一个残量网络上,所以我们就可以使用 dfs 直接进行增广。但是反向边的剩余流量还是需要计算的,因为在将关键边的剩余流量设为 之后,dfs 可能还是会将贡献再次计算。
阻塞流
Dinic 的关键就是阻塞流,因为每次进行增广操作我们都会将所有的增广路,所以说与 Edmonds-Karp 算法一样,在进行了一次操作时候深度一样的所有增广路都被破坏了,就像下图。
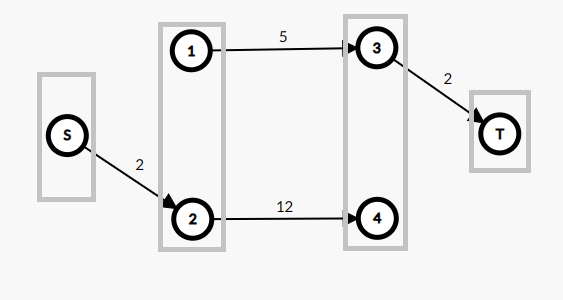
先这样的破坏增广路,我们就称之为阻塞流。
理论上的时间复杂度
因为每一次操作都会将所有的增广路全部榨干,所以增广路的长度必然是严格递增的,所以一共只会进行 次增广操作。而对于 dfs,其时间复杂度为 ,所以总共的时间复杂度为 ,十分优秀。
理论上的实现
int Dinic(int s,int t){
int ans=0;
while(BFS(s,t))
ans+=DFS(s,INF,t);
return ans;
}
int DFS(int s,int flow,int t){
if(s==t||flow<=0)
return flow;
int rest=flow;
for(Edge* i=head[s];i!=NULL&&rest>0;i=i->next){
if(i->flow>0&&depth[i->to]==depth[s]+1){
int k=DFS(i->to,std::min(rest,i->flow),t);
rest-=k;
i->flow-=k;
i->rev->flow+=k;
}
}
return flow-rest;
}
bool BFS(int s,int t){
memset(depth,0,sizeof(depth));
std::queue<int> q;
q.push(s);
depth[s]=1;
while(!q.empty()){
s=q.front();
q.pop();
for(Edge* i=head[s];i!=NULL;i=i->next){
if(i->flow>0&&depth[i->to]==0){
depth[i->to]=depth[s]+1;
if(i->to==t)
return true;
q.push(i->to);
}
}
}
return false;
}
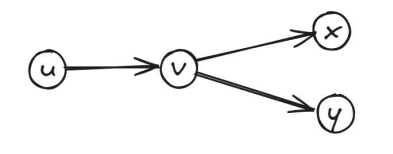
dfs 函数中, 表示现在的位置, 表示汇点,而 则表示因为上游所有流量的最小值,因为所有的流都满足 。接着有一个局部变量 ,表示上游的流量限制还有 单位没有下传。因为要满足流量守恒,我们只能把流入的流量分配到后面,所以这个 实际上保存的就是最大可能的流入流量。最后返回的的 的意思就是在将所有的后继节点全部访问了之后一九无法排除的流,应该让答案减去这个这个贡献。
问题
在增广路的同时我们还面临了一个问题没使用阻塞 dfs 求解增广路其实与使用 bfs 求解的 Edmonds-Karp 完全不同,因为使用阻塞 dfs 会导致一些点需要重复计算,所以在写 dfs 的时候不可以打 标记。
对于下图,在某些特定的流量设计下 好节点就一定需要多次访问。
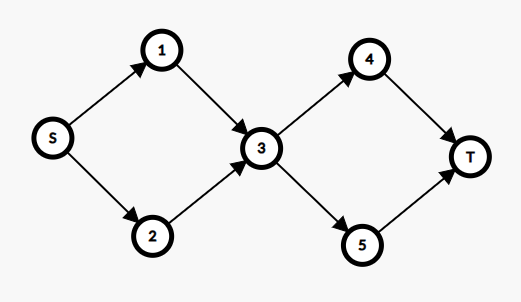
因为 dfs 不使用 标记是指数级别的,所以我们需要进行一些优化。
实现
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
#define int long long
using namespace std;
const int N=205,inf=0x3f3f3f3f3f3f3f3f;
int n,m,s,t,ans,dep[N],p[N];
struct node{int x,v,id;};
vector<node> v[N];
void add(int x,int y,int val){
int o=v[x].size(),p=v[y].size();
v[x].push_back({y,val,p});
v[y].push_back({x,0,o});
}
bool bfs(){
memset(dep,-1,sizeof(dep));
memset(p,0,sizeof(p));
queue<int>q;
q.push(s),dep[s]=0;
while(!q.empty()){
int x=q.front();q.pop();
for(node i:v[x]){
if(dep[i.x]==-1&&i.v){
dep[i.x]=dep[x]+1;
q.push(i.x);
}
}
}
return dep[t]!=-1;
}
int dfs(int x,int flow){
int tmp=flow;
if(!flow||x==t) return flow;
for(int id=p[x];id<v[x].size()&&tmp;id++){
p[x]=id;node &i=v[x][id];
if(dep[i.x]==dep[x]+1&&i.v>0){
int t=dfs(i.x,min(i.v,tmp));
if(!t){
dep[i.x]=-1;
}
else{
i.v-=t,tmp-=t;
v[i.x][i.id].v+=t;
}
}
}
return flow-tmp;
}
int dinic(){
while(bfs()){
ans+=dfs(s,inf);
}
return ans;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m>>s>>t;
for(int i=1,x,y,v;i<=m;i++){
cin>>x>>y>>v;
add(x,y,v);
}
cout<<dinic()<<'\n';
return 0;
}
真实的求解
首先需要明确,将 设置为 就是将其删除的意思,因为不可能有 为 的节点。因为如果尝试给我们忽略掉的点推送一个非 的流量,那么他一定只会返回 ,一点用都没有。
然后最关键的决定时间复杂度的优化是当前弧优化,我们每次向某条边的方向推流的时候,肯定要么把推送量用完了,么是把这个方向的容量榨干了。
除了最后一条因为推送量用完而无法继续增广的边之外其他的边一定无法继续传递流量给 了。这种无用边会在寻找出边的循环中增大时间复杂度,必须删除。
最后再看重新这一整个 DFS 的过程,如果当前路径的最后一个点可以继续扩展,则肯定是在层间向汇点前进了一步,最多走 步就会到达汇点. 在前进过程中,我们发现一个点无法再向 传递流量,我们就删掉它. 根据我们在分析EK算法时间复杂度的时候得到的结论,我们会找到 条不同的增广路,每条增广路又会前进或后退 步来更新流量,又因为我们加了当前弧优化所以查找一条增广路的时间是和前进次数同阶的,于是单次阻塞增广 DFS 的过程的时间上界是 的.
于是 Dinic 算法的总时间复杂度是 的。
二分图最大匹配
问题
给定一个二分图 ,即分左右两部分,各部分之间的点没有边连接,要求选出一些边,使得这些边没有公共顶点,且边的数量最大。
解决方法
保留原有部分的连边,将所有连边设为从左向右的容量为 的有向边。将 用容量为 的边连接所有左边的节点,把所有右边的节点用容量为 的边连向 。
二分图多重匹配
问题
给定一个二分图 ,即分左右两部分,各部分之间的点没有边连接,要求选出一些边,使得每一个点连接的边不超过其上限,且边的数量最大。
解决方法
所有连边方法与二分图最大匹配一致,唯一的不同点就在于与 与 连边的容量为这个点连接的边的上限。
最小不相交路径覆盖
路径的定义
对于一条迹 ,若其连接的点的序列中点两两不同,则称 是一条路径。
注意:一个节点本身也是路径
问题
给定一个有向无环图,找出最少的路径使得这些路径覆盖所有点,并且要求这些路径没有交点。
解决方法
我们可以将 个点拆成 个点,分别作为图的左部与右部。其中编号为 到 的为左部,编号为 到 的为右部。对于原图中的边 将 到 连边,得到一个拆点二分图。得到的 。
证明
对于任意一个路径,除了起点和终点分别只有一个后继和前驱之外,每一个节点都有前驱和后继。对于每个点 ,将其拆分成两个点 和 ,其中 代表前驱节点。 代表后驱节点,即二分图的左部分和右部分。
为了让最小路径覆盖最小,应该让二分图尽可能连接的边多,即二分图最大匹配。给每个点找到他的前驱和后继,对应选择二对于左部分没有匹配的节点,表示没有后继,对应路径的终点。这样的点的数量就是原图点个数 二分图的最大匹配数。右部分没有匹配的节点,表示没有前驱,对应路径的起点。因此 。
最小不相交路径覆盖
问题
给定一个有向无环图,找出最少的路径使得这些路径覆盖所有点,不强制要求这些路径没有交点。
传递闭包
传递闭包可以使用 floyd 求解,其中 不表示从 到 的最短距离,而表示 是否可以到大 。
解决方法
使用 Floyd 进行传递闭包,如果 那么增加边 ,然后对这个新建出的图进行最小不相交路径覆盖即可。
证明
因为原图在求解 时可能会与其他的边相交导致路线出现相交的情况,但是一旦将 连接起来,那么 的路径就可以直接通过 到达,并不会出现问题。
最小割
定义
给定一个网络 ,在边集中选择一些边删除使得源点 与汇点 不连通。定义删除边 的代价为 ,则最小割即即使对于所有的割,删除的边代价最小和。
最大流最小割定理
内容
对于一个网络流图 ,其中有源点 和汇点 ,那么下面三个条件是等价的:
- 流 是图 的最大流
- 残量网络 不存在增广路
- 对于 的某一个割 ,此时流 的流量等于其容量
证明
増广路算法基础, 正确性显然。割的容量是流量的上界, 正确性显然。
然后证明 。
假设残留网络 不存在增广路,所以在残留网络 中不存在路径从 到达 。
我们定义 集合为:当前残留网络中 能够到达的点。同时定义 。此时 构成一个割 。且对于任意的 ,边 必定满流。若边 不满流,则残量网络中必定存在边 ,所以 可以到达 ,与 属于 矛盾。
因此有 。
最多限制相交路径
问题
已知一些路径,每一个节点可以属于多个路径,但是属于路径的数量不得超过一个给定的上限。
解决方法
将 个节点拆为 个,接着进行连边,其中容量代表可以经过的路径。
最大权闭合图
定义
如果一个点集满足其中任意元素可以到达的所有元素都在集合中,那么这个点集中的节点可以经过的边和节点构成的图被称为闭合图。最大权闭合图指对于所有的闭合图,点权和最大的图就是最大权闭合图。
对于下图,最大权闭合图为 ,其权值为 。
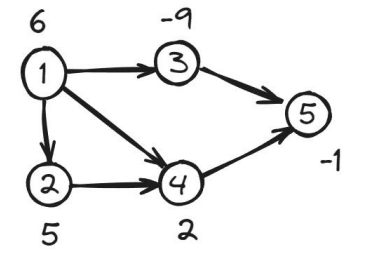
求解方法
新建源点 与汇点 ,让 向所有点权为正的节点连一条容量为点权的边,接着让所有点权为负的点向 连一条容量为点权的绝对值的边。在将图中原有的边设为无穷大之后,求出最小割。
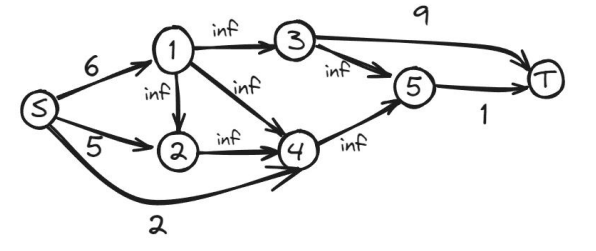
有定理:。
证明
通过上述方式构造,最小割中的所有边均与 或者 ,因为其他的点均被设置为了无穷大,肯定不会选择。
假设在删除割之后, 可以到大的点为图 ,在图 中删除与 相连的边与 节点后构成的图 就是一个最大权闭合图。
设割集中,连接到点 的点权和为 ,连接到点 的点权和为 ,割集的和为 。设图 所有点的点权和为 ,其中正权和为,负权和为,有。
则 ,其中 ,因为图 所有负权点都连接到 ,而为了保证 中的点都不与 连通,这些负权点与 相连的边都删除了,在割集中。
得到 ,移项有 ,其中 为所有正权点之和,要想 最大,那么 最小,则 为最小割。
最小点权覆盖集
问题
在图中选取一些点,满足图中每条边连接的两个点中,至少一个被选择,求所选取的点最小权值和。
求解方法
首先对图进行二分染色,将点分为左部分和右部分。新建源点 和汇点 , 向左部节点连边,容量为点权,右部向 连边,容量为点权,图中原有边的容量设为无穷大。对新图求解最小割就是最小点权覆盖集。
证明
对于任意一条从 到 的路径,一定存在一条边被割断,而且因为原图对应的边容量为无穷大,因此割边必然存在于 与左部节点之间或者右部节点与 之间,对应的流量便是选取的最小点权。
在图中选取一些点,满足图中每条边连接的两个点中,至多一个被选择,求所选取的点最大权值和。
定理:
证明:因为点权覆盖集对于原图的点集的补集即为点权独立集,而点集的点权之和为常数,所以当点权覆盖集最小时,点权独立集最大,对应的答案即为所有点权值和-最小点权覆盖集。
费用流
定义
给定一个有 个点 条边的网络,每条边有一个容量限制 和一个使用的代价 。当边 使用的流量为 时,其花费的代价为 。这个网络中总共代价最少的最大流被称为最小费用最大流,总共代价最多的最大流被称为最大费用最大流。
注意:费用流是建立在最大流的基础上的,让流量的大小是第一关键字。
求解
因为最大流是一样的,所以依然可以套用 Dinic 的思路。因为 Dinic 的增广路长度是可以贪心的寻找的,所以只要每一次增广路的费用最小,那么就可以让费用最小。所以我们可以将将代价看作边权,把原本的 bfs 换成 spfa 找最短路。
如果需要求解费用最大最大流,那么只需要将所有的边取反,再跑一次费用最小最大流就可以了。
实现
#include<iostream>
#include<cstring>
#include<queue>
#include<vector>
#include<bitset>
#define int long long
using namespace std;
const int N=5e3+5,inf=0x3f3f3f3f3f3f3f3f;
int n,m,s,t,ans,sum,dep[N],p[N];
bitset<N>vis;
struct node{
int x,v,w,id;
};
struct dog{
int x,v;
friend bool operator < (const dog a,const dog b){
return a.v>b.v;
}
}top;
vector<node> v[N];
void add(int x,int y,int val,int w){
int sx=v[x].size(),sy=v[y].size();
v[x].push_back({y,val,w,sy});
v[y].push_back({x,0,-w,sx});
}
bool bfs(){
memset(dep,0x3f,sizeof(dep));
memset(p,0,sizeof(p));
priority_queue<dog> q;
q.push({s,0}),dep[s]=0;
while(!q.empty()){
top=q.top(),q.pop();
if(dep[top.x]!=top.v) continue;
for(node i:v[top.x]){
if(dep[i.x]>dep[top.x]+i.w&&i.v){
dep[i.x]=dep[top.x]+i.w;
q.push({i.x,dep[i.x]});
}
}
}
return dep[t]!=inf;
}
int dfs(int x,int flow){
if(!flow||x==t) return flow;
int tmp=flow;vis[x]=1;
for(int id=p[x];id<v[x].size()&&tmp;id++){
p[x]=id;node &i=v[x][id];
if(!vis[i.x]&&dep[i.x]==dep[x]+i.w&&i.v>0){
int t=dfs(i.x,min(i.v,tmp));
if(!t) dep[i.x]=-1;
else{
i.v-=t,tmp-=t;
v[i.x][i.id].v+=t;
sum+=i.w*t;
}
}
}
vis[x]=0;
return flow-tmp;
}
int dinic(){
int ans=0;
while(bfs()){
ans+=dfs(s,inf);
}
return ans;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m>>s>>t;
for(int i=1,x,y,v,w;i<=m;i++){
cin>>x>>y>>v>>w;
add(x,y,v,w);
}
cout<<dinic()<<' '<<sum<<'\n';
return 0;
}
二分图最大权匹配
问题
选择一些边,如果满足任意两条边都没有公共端点,那么这些边被称为二分图的一组匹配。二分图最大权匹配就是寻找所有的二分图的匹配中权最大的,注意权最大是第一关键字,而是否是匹配最多的无关紧要。
求解方法
首先,在图中新增源点 与汇点 。从 的每个做部分开始连接一条流量为 的边,其费用为 。从每一个二分图右侧的节点连一条流量为 的边到 ,其费用同样为 。
接下来,如果二分图原本有一条边 的边权为 的边,那么就从 连一条流量为 费用为 的边到 。
但是如果直接跑一个最大费用最大流是错误的,因为最大费用最大流是在满足最大流的基础上求解的,但是流量最大其权并不一定是最大的,与二分图最大权匹配的要求权最大相矛盾。
因为对于所有的左部节点,还需要连接一条有这个节点到 的边,流量为 ,费用为 。再求解这个图的费用流即可得到答案。
上下界网络流
定义
上下界网络流就是在原本网络流的基础上添加了每一条边流量的上界 和下界 ,也就是说 必须满足 。
无源汇上下界可行流
无源汇界网指的是没有源点和汇点但是每一个点的出边与入边都满足流量守恒的网络。在这个网络的流量方案中,应使得第 条边的流量位于 之间。
换而言之流量 必然满足 ,而普通的网络流只满足 。
所以根据不等式的性质,我们可以得到 ,于是上下界网络流就被转化为了普通网络流。
但是这样求解的网络的流量不一定是守恒的,就像下面的情况:
对于普通网络流,设 表示流入 的流量, 表示流出 的流量,所以有 。在经过修改之后, 变为了 ,而 变为了 。因为并不知道 是否等于 ,所以无法确定流量是守恒的。
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#define int long long
using namespace std;
const int N=2e5+5,inf=0x3f3f3f3f3f3f3f3f;
struct node{int x,v,id;};
vector<node> v[N];
int n,m,s,t,dep[N],p[N];
void add(int x,int y,int val){
int sti=v[x].size(),edi=v[y].size();
v[x].push_back({y,val,edi});
v[y].push_back({x,0,sti});
}
bool bfs(){
queue<int> q;
memset(dep,-1,sizeof(dep));
memset(p,0,sizeof(p));
q.push(s),dep[s]=0;
while(!q.empty()){
int top=q.front();q.pop();
for(node i:v[top]){
if(dep[i.x]==-1&&i.v){
dep[i.x]=dep[top]+1;
q.push(i.x);
}
}
}
return dep[t]!=-1;
}
int dfs(int x,int flow){
if(x==t||!flow){
return flow;
}
for(int i=p[x];i<v[x].size();i++){
p[x]=i;
int to=v[x][i].x,len=v[x][i].v;
if(dep[x]+1==dep[to]&&len){
int t=dfs(to,min(len,flow));
if(t){
v[x][i].v-=t;
v[to][v[x][i].id].v+=t;
return t;
}
else{
dep[to]=-1;
}
}
}
return 0;
}
int dinic(){
int ans=0,flow;
while(bfs()){
ans+=dfs(s,inf);
}
return ans;
}
int a[N],f[N],cnt[N];
vector<int> ask;
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m,t=n+1;
for(int i=1,x,y,l,r;i<=m;i++){
cin>>x>>y>>l>>r;
a[i]=l,f[x]-=l;f[y]+=l;
add(x,y,r-l),ask.push_back(x);
}
int sum=0;
for(int i=1;i<=n;i++){
if(f[i]>0){
add(s,i,f[i]),sum+=f[i];
}
if(f[i]<0){
add(i,t,-f[i]);
}
}
if(dinic()!=sum){
cout<<"NO\n";
}
else{
cout<<"YES\n";
for(int i=1;i<=m;i++){
cout<<a[i]+v[v[ask[i-1]][cnt[ask[i-1]]].x][v[ask[i-1]][cnt[ask[i-1]]].id].v<<'\n';
// cout<<ask[i-1]<<' '<<v[ask[i-1]][cnt[ask[i-1]]].x<<'\n';
cnt[v[ask[i-1]][cnt[ask[i-1]]].x]++;
cnt[ask[i-1]]++;
}
}
return 0;
}
有源汇上下界可行流
为了保证流量守恒,如果 ,那么就新建一个源点 到 的容量为 来弥补流量的不足。反之如果 ,那么就同理建一个从 到汇点 的容量为 来帮助 排除多出的流量。
因为流量守恒,所以我们新连的边一定要跑满,即求解新的网络的最大流是否等于所有 的出边的容量的和。定义可行流的流量是残留网络的反向边的大小加上减去的下界 ,注意这是残留网络,反向边的流量大小是原图的流量。
在有源汇网络上求一个流量方案,使得第 条边的流量必须在 之间,且除源汇外每个点流量守恒。
假设源点为 ,汇点为 。则入一条 到 的上界为无穷大,下界为 的边转化为无源汇上下界可行流问题。
若有解,则 到 的可行流流量等于T到S的附加边的流量。
有源汇上下界最大/小流
首先求出一个有源汇有上下界可行流,然后将附加边删除后,在残量网络上跑源点到汇点的最大流,。
再跑一次最大流是因为附加网络上属于原图的边还有流量没被“榨干”。容易发现只要附加网络上不属于原图的边满流,那么属于原图的边怎么跑流量都是守恒的。因为第一次跑最大流已经保证所有点守恒,第二次跑最大流不会经过不属于原图的边,因此等价于对原图跑一次普通的最大流,除源汇外流量守恒。两次合起来总流量一定守恒,这就保证了正确性。
同理求最小流就跑一次汇点到源点的最大流,。这是因为反向边的流量增加等价于正向边的的流量减少。
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
const int N=3e5+5,inf=0x3f3f3f3f;
struct node{int x,v,id;};
vector<node> v[N];
int n,m,s,t,dep[N],p[N];
void add(int x,int y,int val){
int sti=v[x].size(),edi=v[y].size();
v[x].push_back({y,val,edi});
v[y].push_back({x,0,sti});
}
bool bfs(){
queue<int> q;
memset(dep,-1,sizeof(dep));
memset(p,0,sizeof(p));
q.push(s),dep[s]=0;
while(!q.empty()){
int top=q.front();q.pop();
for(node i:v[top]){
if(dep[i.x]==-1&&i.v){
dep[i.x]=dep[top]+1;
q.push(i.x);
}
}
}
return dep[t]!=-1;
}
int dfs(int x,int flow){
if(x==t){
return flow;
}
for(int i=p[x];i<v[x].size();i++){
p[x]=i;
int to=v[x][i].x,len=v[x][i].v;
if(dep[x]+1==dep[to]&&len){
int t=dfs(to,min(len,flow));
if(t){
v[x][i].v-=t;
v[to][v[x][i].id].v+=t;
return t;
}
else{
dep[to]=-1;
}
}
}
return 0;
}
int dinic(){
int ans=0,flow;
while(bfs()){
while(flow=dfs(s,inf)){
ans+=flow;
}
}
return ans;
}
int a[N],f[N],cnt[N],S,T;
vector<int> ask;
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m>>S>>T;
t=n+1;
for(int i=1,x,y,l,r;i<=m;i++){
cin>>x>>y>>l>>r;
a[i]=l,f[x]-=l;f[y]+=l;
add(x,y,r-l),ask.push_back(x);
}
int sum=0;
for(int i=1;i<=n;i++){
if(f[i]>0){
add(s,i,f[i]),sum+=f[i];
}
if(f[i]<0){
add(i,t,-f[i]);
}
}
add(T,S,inf);
if(dinic()!=sum){
cout<<"please go home to sleep\n";
}
else{
int ans=v[S][v[S].size()-1].v;
for(int i=1;i<=n;i++){
if(f[i]>0){
v[s].pop_back();
v[i].pop_back();
}
if(f[i]<0){
v[i].pop_back();
v[t].pop_back();
}
}
v[S].pop_back();
v[T].pop_back();
s=T,t=S;
cout<<ans-dinic()<<'\n';
}
return 0;
}
