二叉查找树

二叉查找树是一棵有点权的二叉树，具有以下几个特征：

• 左孩子的权值小于父亲的权值
• 右孩子的权值大于父亲的权值
• 中序遍历及从小到大排序

关于这个性质的证明也很简单（因为有智障包不理解，所以才写的）。

因为中序遍历的顺序是左中右，所以第一个访问的一定是最左边的叶子节点，也一定是最小的。同理，第二个节点一定是他的父亲，也就是比他大的数字中最小的。

二叉查找树支持以下几个操作：

• 插入一个数
• 删除一个数
• 找一个数的前驱
• 找一个数的后继
• 询问一个数的排名
• 询问排第几名的数

二叉查找树一棵二叉查找树，所以在它是一棵完全二叉树时，树的度为 $\log \text{n}$，所以单一操作的时间复杂度应该是 $\text{O(log n)}$ 级别的。但是在进行操作时，如果输入的点权单调递增或递减，那么整个数据结构就将由树退化成为链。所以单次操作的时间复杂度最坏为 $\text{O(n)}$ 级别。

需要理解退化的原因就要先知道二叉搜索树是怎么插入的。在插入时，如果插入的值大于这个节点，那么久访问访问右子树，否则访问左子树。如果在访问子树时访问到了不存在的节点，那么久直接在这里新建一个需要添加的节点。

如果输入的节点依次递增，那么在插入的时候就会一直访问左子树，并且一直在左子树新建节点。二叉树就只有右儿子，所以度就成为了 $\text{n}$。

普通平衡树

为了使这个数据结构平衡，平衡树就应运而生了。Treap 就是平衡树的一种，这个算法就是将树 (Tree) 与堆 (Heap) 相结合了起来。Treap 给每一个节点在维护原来的数值的同时，还添加了一个随机值。但看权值，这是一颗二叉搜索树，但是但看随机值这又是一个堆。

储存

首先我们应该了解一下如何储存一颗平衡树。

因为平衡树的结构是会改变的，所以我们需要储存每一个节点的左孩子与右孩子。因为一个节点可能会多次添加，所以应该使用 cnt 记录以下这个节点出现的个数。为了后面的操作，我们应该还需要定义一个 size 变量记录这个节点及子树的大小。

所以在我们定义的结构体应该是下面这样的：

struct node{
	int l,r,k,val,cnt,size;
}a[N];

updata

在进行修改操作之后，节点的子树大小会发行变化。updata 函数的功能是更新节点的 size 值。

void updata(int u){
	a[u].size=a[a[u].l].size+a[a[u].r].size+a[u].cnt;
}

make

在进行操作时，为了节省空间复杂度，平衡树使用了动态开点。动态开点就是你需要使用一个新节点时就现马上申请一个空间，而不是全部预留好。

int make(int k){
	a[++tot].k=k,a[tot].val=rand(); //tot 记录节点个数
	a[tot].cnt=a[tot].size=1;
	return tot;
}

zig && zag

既然需要再维护二叉查找树的同时维护平衡树，就需要在不改变平衡树的性质的情况下完成堆所需要的 swap 的操作。所以我们就迎来了平衡树最重要的操作 zig 与 zag。

这是一棵平衡树，其中 1 2 3 为节点 A B C 为子树。
它们满足以下性质：1>A>2>C>3>D

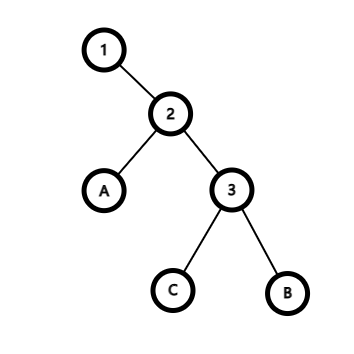
那么如果需要交换 2 3 的位置，那么在不违背其性质的情况下将其改为：

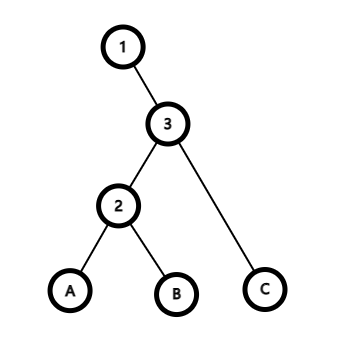
这个过程就是 zig 操作，反之即是 zag 操作。代码实现就是将将操作进行模拟，方法如下：

void zig(int &p){
	int q=a[p].l;
	a[p].l=a[q].r,a[q].r=p,p=q;
	updata(a[p].r),updata(p);
}
void zag(int &p){
	int q=a[p].r;
	a[p].r=a[q].l,a[q].l=p,p=q;
	updata(a[p].l),updata(p);
}

build

因为在平衡树中有旋转操作，所以根节点有可能会在旋转操作中改变位置。为了让根节点的位置保持不变，可以建立两个虚点，并令其优先级远远高于其他的点,永远停留在根节点的位置。

void build(){
	make(-INF),make(INF);
	root=1,a[1].r=2,updata(root);
	if(a[1].val<a[2].val) zag(root);
}

insert

在插入操作中，一共有三种操作。反复执行操作三，直至满足操作一或操作二。

• 操作一：需要处理的节点为 $0$，意味着这个节点不存在，所以直接新建。

• 操作二：已经找到车要添加的节点，cnt++。

• 操作三：需要添加的节点小于或大于这个节点，那么分别访问左节点或右节点。

void insert(int &p,int k){
	if(p==0) p=make(k);
	else{
		if(a[p].k==k) a[p].cnt++;
		if(a[p].k>k){
			insert(a[p].l,k);
			if(a[a[p].l].val>a[p].val) zig(p);
		}if(a[p].k<k){
			insert(a[p].r,k);
			if(a[a[p].r].val>a[p].val) zag(p);
		}
	}updata(p);
}

这是以下是一棵平衡树，其中的节点的信息如下：

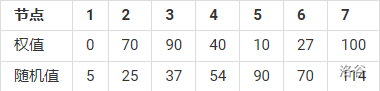
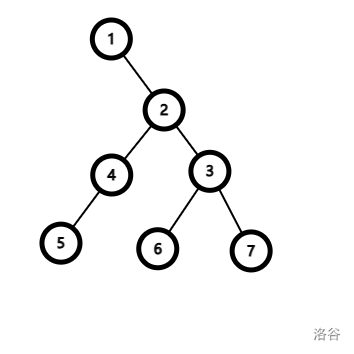
那么如果需要插入一个名为 X 点权为 $50$ 随机值为 $50$ 的节点，那么操作就将是这样的：

• 首先与 $1$ 比较，发现权值大于 $1$ ，移动到右子树 $2$ 号节点。

• 与 $2$ 号节点比较，发现点权小于 $2$ 号节点，那么到左子树 $4$ 号节点。

• 与 $4$ 号节点进行比较，发现点权大于 $4$ 号节点而且右子树为空，所以新建一个节点。

• 开始回溯，发现 $4$ 号节点与节点 $\text{X}$ 的随机值不满足小根堆的要求所以执行旋转操作。

• 在旋转之后，$3$ 号节点的左子树变为节点 $\text{X}$，$\text{X}$ 的左子树为 $4$ 号节点，$4$ 号节点的左子树为 $5$ 号节点。

• 再次回溯，发现以上节点均满足小根堆要求，所以操作完成。

del

在删除操作中，同样分为三种操作：

• 操作一：没有找到这个点就直接返回，不进行修改操作。

• 操作二：如果这个节点的值大于或者小于要删除的值，那么就继续访问左孩子或者右孩子。

• 操作三：找到了这个值，如果 cnt 大于 $1$，那么直接 cnt-- 否则寻找比这个节点大的集合中的最小值。

void del(int &p,int k){
	if(p==0) return ;
	if(a[p].k==k){
		if(a[p].cnt>1){
			a[p].cnt--;
			updata(p);
			return;
		}if(a[p].l||a[p].r){
			if(!a[p].r||a[a[p].l].val) zig(p),del(a[p].r,k);
			else zag(p),del(a[p].l,k);
		}else p=0;
		updata(p);
		return;
	}if(a[p].k>k) del(a[p].l,k);
	else del(a[p].r,k);
	updata(p);
}

这是以下是一棵平衡树，其中的节点的信息如下：

那么如果需要将权值为 $70$ 的节点删除，那么操作就是这样的：

• 首先与 $1$ 号节点进行对比，发现权值小于 $1$ 号节点，进入左子树。

• 与 $2$ 号节点比较，发现权值等于 $2$ 号节点，寻找权值大于 $70$ 且最小的点。

• 首先向左走一步，来到 $3$ 号节点。

• 进入 $3$ 号节点左子树 $6$ 号节点。

• $6$ 号节点没有左子树，所以 $6$ 号节点就是要寻找的目标点。

• 让 $6$ 号节点取代 $2$ 号节点的位置，操作结束。

get_rank

get_rank 函数可以获得某个点的排名。在寻找时如果节点在左子树，则这个节点在左子树的排名就是这个节点在这棵子树上的排名。反之，如果这个节点在右子树，那么他的排名就是左子树的大小+根节点的大小+自己在右子树的排名。

int get_rank(int p,int k){
	if(p==0) return 0;
	if(a[p].k==k) return a[a[p].l].size+1;
	if(a[p].k>k) return get_rank(a[p].l,k);
	return a[a[p].l].size+a[p].cnt+get_rank(a[p].r,k);
}

因为查询的数可能不在树中存在，所以但是 get_rank 的返回值又是默认其存在的，所以将答案设为了函数值$-1$。为了避免发生这样的错误，需要在定义一个 find 函数检查是否存在这个节点。

bool find(int p,int x){
	if(a[p].k==x) return 0;
	if(a[p].val==0) return 1;
	if(a[p].k>x) return find(a[p].l,x);
	return find(a[p].r,x);
}

get_key

get_key 函数可以获取某个排名的数。当访问到一个节点时，如果这个节点的左子树的大小大于它的排名，那么这个节点就应该在左子树。如果这个排名大于这个节点的大小 + 左子树的大小，那么这个节点就应该在右子树。其他的情况就应该就在这个节点。

int get_key(int p,int rank){
	if(p==0) return INF;
	if(a[a[p].l].size>=rank) return get_key(a[p].l,rank);
	if(a[a[p].l].size+a[p].cnt>=rank) return a[p].k;
	return get_key(a[p].r,rank-a[a[p].l].size-a[p].cnt);
}

get_pr

get_pr 函数可以找到一个数的前驱，及比他大的数中最小的一个。因为平衡树满足左孩子 $<$ 根节点 $<$ 右孩子，所以只需要先走到左孩子，再一直向右走就可以了。

int get_pr(int p,int k){
	if(p==0) return-INF;
	if(a[p].k>=k) return get_pr(a[p].l,k);
	return max(get_pr(a[p].r,k),a[p].k);
}

get_ne

get_ne 函数可以找到一个数的后驱，及比他小的数中最大的一个。因为平衡树满足左孩子 $<$ 根节点 $<$ 右孩子，所以只需要先走到右孩子，再一直向左走就可以了。

int get_ne(int p,int k){
	if(p==0) return INF;
	if(a[p].k<=k) return get_ne(a[p].r,k);
	return min(get_ne(a[p].l,k),a[p].k);
}

P3369 普通平衡树

这一题就是一道模板题，只需要将前面的操作整合在一起就可以了。

#include<bits/stdc++.h>
using namespace std;
const int N=100010,INF=1e8;
int n;
struct Node{int l,r,k,val,cnt,size;}a[N];
int root,tot;
void updata(int u){a[u].size=a[a[u].l].size+a[a[u].r].size+a[u].cnt;}
int make(int k){
	a[++tot].k=k,a[tot].val=rand();
	a[tot].cnt=a[tot].size=1;
	return tot;
}
void zig(int &p){
	int q=a[p].l;
	a[p].l=a[q].r,a[q].r=p,p=q;
	updata(a[p].r),updata(p);
}
void zag(int &p){
	int q=a[p].r;
	a[p].r=a[q].l,a[q].l=p,p=q;
	updata(a[p].l),updata(p);
}
void build(){
	make(-INF),make(INF);
	root=1,a[1].r=2,updata(root);
	if(a[1].val<a[2].val) zag(root);
}
void insert(int &p,int k){
	if(p==0) p=make(k);
	else{
		if(a[p].k==k) a[p].cnt++;
		if(a[p].k>k){
			insert(a[p].l,k);
			if(a[a[p].l].val>a[p].val) zig(p);
		}if(a[p].k<k){
			insert(a[p].r,k);
			if(a[a[p].r].val>a[p].val) zag(p);
		}
	}updata(p);
}
void del(int &p,int k){
	if(p==0) return ;
	if(a[p].k==k){
		if(a[p].cnt>1){
			a[p].cnt--;
			updata(p);
			return;
		}if(a[p].l||a[p].r){
			if(!a[p].r||a[a[p].l].val) zig(p),del(a[p].r,k);
			else zag(p),del(a[p].l,k);
		}else p=0;
		updata(p);
		return;
	}if(a[p].k>k) del(a[p].l,k);
	else del(a[p].r,k);
	updata(p);
}
int get_rank(int p,int k){
	if(p==0) return 0;
	if(a[p].k==k) return a[a[p].l].size+1;
	if(a[p].k>k) return get_rank(a[p].l,k);
	return a[a[p].l].size+a[p].cnt+get_rank(a[p].r,k);
}
int get_key(int p,int rank){
	if(p==0) return INF;
	if(a[a[p].l].size>=rank) return get_key(a[p].l,rank);
	if(a[a[p].l].size+a[p].cnt>=rank) return a[p].k;
	return get_key(a[p].r,rank-a[a[p].l].size-a[p].cnt);
}
int get_pr(int p,int k){
	if(p==0) return-INF;
	if(a[p].k>=k) return get_pr(a[p].l,k);
	return max(get_pr(a[p].r,k),a[p].k);
}
int get_ne(int p,int k){
	if(p==0) return INF;
	if(a[p].k<=k) return get_ne(a[p].r,k);
	return min(get_ne(a[p].l,k),a[p].k);
}
bool find(int p,int x){
	if(a[p].k==x) return 0;
	if(a[p].val==0) return 1;
	if(a[p].k>x) return find(a[p].l,x);
	return find(a[p].r,x);
}
int main(){
	build();
	cin>>n;
	for(int i=1,op,x;i<=n;i++){
		cin>>op>>x;
		if(op==1) insert(root,x);
		if(op==2) del(root,x);
		if(op==3) cout<<get_rank(root,x)+find(root,x)-1;
		if(op==4) cout<<get_key(root,x+1);
		if(op==5) cout<<get_pr(root,x);
		if(op==6) cout<<get_ne(root,x);
		if(op!=1&&op!=2)cout<<endl;
	}return 0;
}