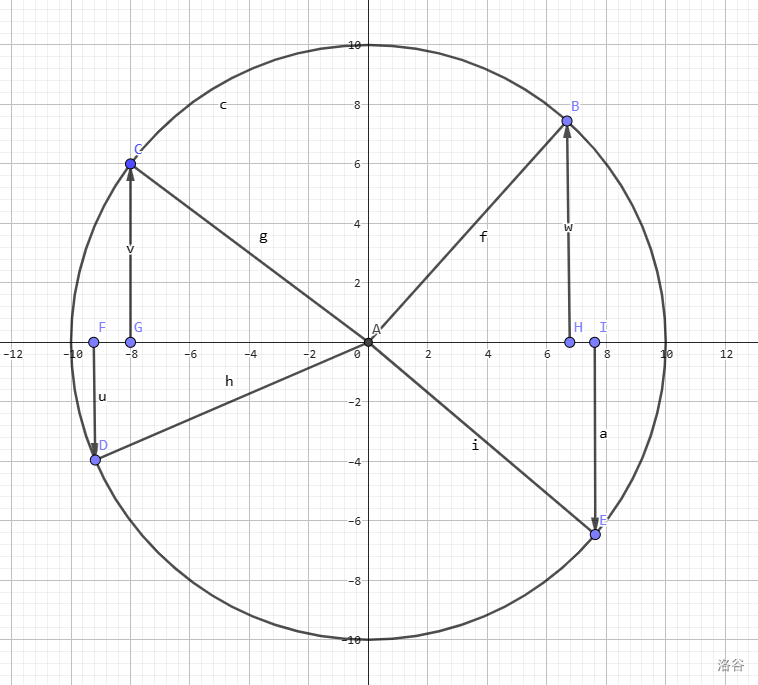
关于上图的解释

图中的圆半径为 11 且原点为 (0,0)(0,0)，对于圆中讨论的三角形都是以从 (0,0)(0,0) 出发平行与 xx 轴的半径长度的边为直角边之一的三角形，所有在 sin⁡\sin 中提及的夹角的顶点均是 (0,0)(0,0)。

0°≤α≤90°0\degree \le \alpha \le 90\degree

这是 sin⁡\sin 最基础的定义，其定义为与夹角所对的直角边与斜边的比。因为图中的斜边全部为 11，所以sin⁡\sin 值就是直角边的长度。

对于 0°≤sin⁡≤90°0\degree \le \sin\le 90\degree 的情况中，对于上图 sin⁡\sin 值就是 ∣HB∣|HB|。

90°≤α≤180°90\degree\le \alpha\le 180\degree

因为向量 GC→\overrightarrow{GC} 的方向为正方先，所以显然 sin⁡\sin 值应该是正数。做 CC 点关于 yy 轴的对称点 CC。易得 GC→\overrightarrow{GC} 的值等于 G′C′→\overrightarrow{G'C'}，所以 sin⁡(α)=sin⁡(α−14π)\sin(\alpha)=\sin(\alpha-\dfrac{1}{4}\pi) 。

180°≤α≤270°180\degree \le \alpha \le 270\degree

观察得到 FD→\overrightarrow{FD} 为负方向，所以容易得到 sin⁡(α)\sin(\alpha) 是一个负数。通过类似于上面的证明方式可以得到 sin⁡(α)=−sin⁡(α−12π)\sin(\alpha)=-\sin(\alpha-\dfrac{1}{2}\pi)。

270°≤α≤360°270\degree \le \alpha \le 360\degree

容易观察到 sin⁡(α)=sin⁡(α−14π)\sin(\alpha)=\sin(\alpha-\dfrac{1}{4}\pi)，所以在化简之后得到 sin⁡(α)=−sin⁡(π−α)\sin(\alpha)=-\sin(\pi-\alpha)。

综上所述

sin⁡(α){sin⁡(α)0°≤α≤90°sin⁡(α−14π)90°≤α≤180°−sin⁡(α−12π)180°≤α≤270°−sin⁡(π−α)270°≤α≤360°\sin(\alpha)\left\{\begin{matrix}\sin(\alpha) & 0\degree \le \alpha \le 90\degree\\\sin(\alpha-\dfrac{1}{4}\pi) & 90\degree\le \alpha\le 180\degree\\-\sin(\alpha-\dfrac{1}{2}\pi) & 180\degree \le \alpha \le 270\degree\\-\sin(\pi-\alpha) & 270\degree \le \alpha \le 360\degree\end{matrix}\right.