一大堆错，别喷了。

前言

下图取自某人的 PPT，有删改。

题面

APIO2014 序列分割

题目大意

你正在玩一个关于长度为 $n$ 的非负整数序列的游戏，第 $i$ 个位置的值为 $a_i$。

这个游戏中你需要把序列分成 $k + 1$ 个非空的块，为了得到 $k + 1$ 块，你需要重复下面的操作 $k$ 次：

• 选择一个有超过一个元素的块（初始时你只有一块，即整个序列）。

• 选择两个相邻元素把这个块从中间分开，得到两个非空的块。

每次操作后你将获得那两个新产生的块的元素和的乘积的分数，你想要最大化最后的总得分。

数据范围

$2 \le n \le 10^5$，$1 \le k \le \min\{n - 1, 200\}$。

闲话：pjt 问我 T1 是什么，我说是动态规划板子，这很合理。

CF1517G Starry Night Camping

题目大意

有 $n$ 顶帐篷，第 $i$个帐篷位于点 $(x_i, y_i)$ 上，权值为 $w_i$。当且仅当 $x_i$ 和 $y_i$ 都是偶数时，帐篷 $i$ 才是重要的。

移除一些帐篷，使得对于每个剩余的重要帐篷 $(x, y)$，不存在另外 $3$ 个帐篷 $(x' _ 1, y' _ 1),(x' _ 2, y' _ 2)$ 和 $(x' _ 3, y' _ 3)$，使得以下两个条件都成立：

• $|x'_j-x|,|y'_j-y|\le 1$，对于所有 $j\in\{1,2,3\}$。

• 这四个帐篷形成一个平行四边形（或矩形），它的一条边平行于 $x$ 轴。

将未移走的帐篷权值之和最大化，输出最大值。

数据范围

$1\le n\le 1000$，$-10^9\le x_i,y_i\le 10^9$，$1\le w_i\le 10^9$。

CF1983E I Love Balls

题目大意

Alice 和 Bob 在玩游戏。他们面前有 $n$ 个球，第 $i$ 个球的价值为 $v_i$，且前 $k$ 个球为“特殊球”，Alice 为先手。

每一轮，Alice 或 Bob 会随机从剩余的球中选取一个球并把它取出，获得它的价值。

如果这个球为特殊球，则下一轮的玩家不变，否则下一轮的玩家改变。

问 Alice 和 Bob 各自得到的价值的期望对 $10^9 + 7$ 取模的值。

数据范围

多测，$1\le T\le 2\times 10^5$，$1\le k\le n\le 4\times 10^5$，$1\le v_i\le 10^7$。

CEOI2017 Building Bridges

有 $n$ 根柱子依次排列，每根柱子都有一个高度。第 $i$ 根柱子的高度为 $h_i$。

现在想要建造若干座桥，如果一座桥架在第 $i$ 根柱子和第 $j$ 根柱子之间，那么需要 $(h_i-h_j)^2$ 的代价。

在造桥前，所有用不到的柱子都会被拆除，因为他们会干扰造桥进程。第 $i$ 根柱子被拆除的代价为 $w_i$，注意 $w_i$ 不一定非负，因为可能政府希望拆除某些柱子。

现在政府想要知道，通过桥梁把第 $1$ 根柱子和第 $n$ 根柱子连接的最小代价。注意桥梁不能在端点以外的任何地方相交。

数据范围

$2\le n\le 10^5$，$0\le h_i,\vert w_i\vert\le 10^6$。

CF1278F Cards 加强

题目大意

有 $m$ 张牌，其中一张是王牌。

现在你执行 $n$ 次右侧操作：洗牌后查看第一张牌是什么。

令 $x$ 为洗牌后第一张牌为王牌的次数，现在假设洗牌时 $m!$ 种牌的排列出现的概率均相等，求 $x^k$ 的期望值，答案对 $998244353$ 取模。

数据范围

$1\le n,m\le 998244353$，$1\le k\le 10^7$。

闲话：本来的范围 $k\le 5000$。

gym 102331 J Jiry Matchings

题目大意

给定一棵树 $n$ 个节点的有边权的树，求对于 $k\in[1,n]\cap\mathbb{Z}$ 的大小为 $k$ 的匹配的最大权值。

一个图的匹配就是在一张图上选择一些边，要求这些边没有公共的端点。

数据范围

$1\le n\le 2\times 10^5$，时限 $2s$。

solution

APIO2014 序列分割

容易得到一个性质：

同样的切法得到的答案都是一样的，换而言之切的顺序与答案无关。

容易证明，设我们把三段和为 $D,C,Z$ 的三段切开，那么：

• 先切 $C,Z$ 的贡献为：$(D+C)\times Z+D\times C$，也就是 $DC+DZ+CZ$。
• 先切 $D,C$ 的贡献为：$D\times (C+Z)+C\times Z$，也就是 $DC+DZ+CZ$。

设 $s_i=\sum\limits_{i=1}^i a_i$，$F_{i,j}$ 表示前 $i$ 次切割 $j$ 次可以得到的贡献的最大值，注意这个的状态数是 $O(nk)$ 的如果 $O(1)$ 转移是可以通过的。

我们记 $f_k=F_{i,k}$，$g_k=F_{i-1,k}$，那么显然有转移方程：

$f_i=\max\{g_j+s_j\times (s_i-s_j)\}$

显然添加的第 $[i,j]$ 段会和前面所有的段都发生贡献，所以需要乘以 $s_j$。

观察，Z_drj 都可以看出来可以斜率优化。

我们取任意的 ${j1}\lt {j2}$ 且满足 $f_i$ 的决策点是 ${j2}$ 优于 ${j1}$，那么就可以得到下面的不等式：

$g_{j2}+s_{j2}\times (s_i-s_{j2})\gt g_{{j1}}+s_{{j1}}\times (s_i-s_{j1})$

整理一下得到：

$(s_i\times s_{j2})+(g_{{j2}}-{s_{{j2}}}^2)\gt (s_i\times s_{j1})+(g_{{j1}}-{s_{{j1}}}^2)$

移项：

$s_i\times (s_{j2}-s_{j1})\gt g_{{j1}}-{s_{{j1}}}^2-g_{{j2}}+{s_{{j2}}}^2$

因为 $s_{j2}\gt s_{j1}$，所以有：

$-s_i\lt \dfrac{(g_{{j2}}+{s_{{j2}}}^2)-(g_{{j1}}-{s_{{j1}}}^2)}{s_{j2}-s_{j1}}$

总结一下，如果上面的式子成立那么 $j2$ 比 $j1$ 要优。

考虑建立一个直角坐标系，把 $s$ 作为 $X$ 坐标，把 $g+s^2$ 作为 $Y$ 坐标，那么每一个决策就都成为了一个点。

假设有三个决策点 $D,C,Z$，他们的斜率分别是 $k_1$ 和 $k_2$，且 $k_0$ 是 $-s_i$，满足下图：

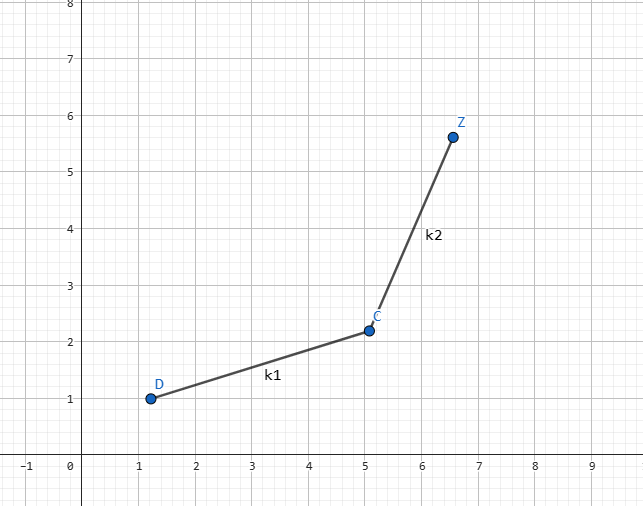
那么根据我们上面得到的式子有：

• 如果 $k_0<k_1$，那么 $C$ 比 $D$ 优。
• 如果 $k_0<k_2$，那么 $Z$ 比 $C$ 优。
• 观察得到 $k_1<k_2$，即上图是一个下凸。

那么有三种情况：

• $k_0<k_1<k_2$，那么 $Z$ 比 $C$，$D$ 优。
• $k_1<k_0<k_2$，那么 $D$，$Z$ 比 $C$ 优。
• $k_1<k_2<k_0$，那么 $D$ 比 $C$，$Z$ 优。

发现 $C$ 太逊了，也就是在这个情况下是决策点永远不可能是下凸。

因为永远不可能是下凸，所以肯定是上凸（好像这句话是废话）。

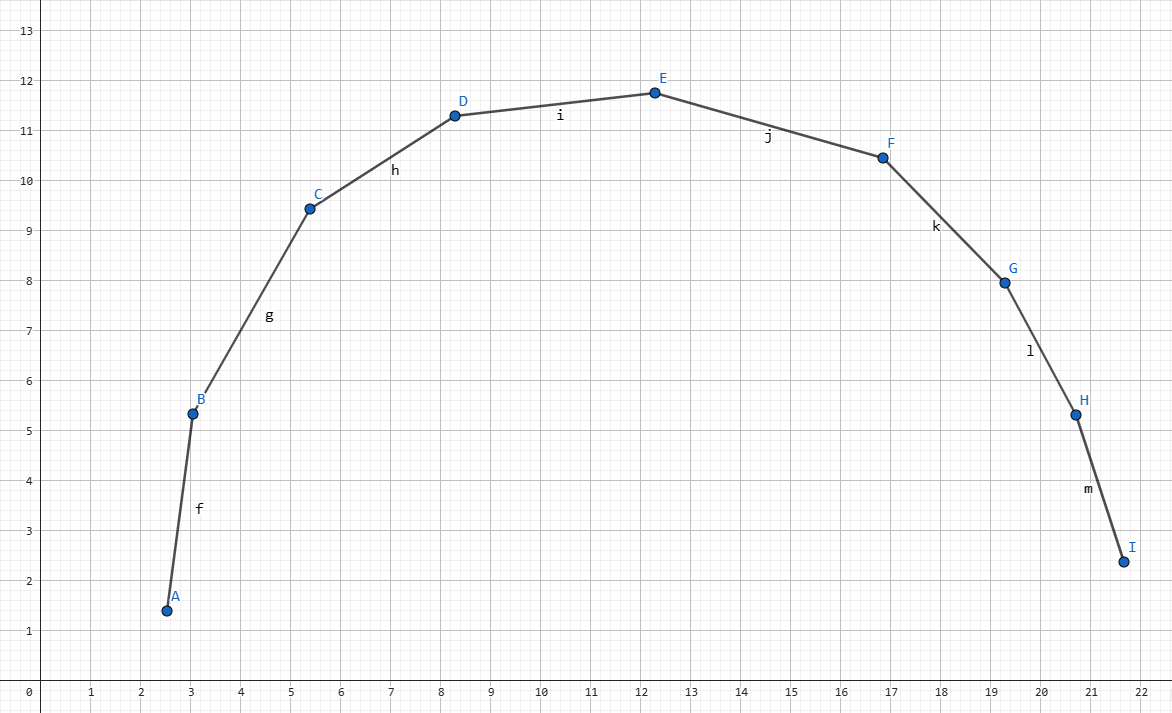
显然，如果决策点 $k$ 被选择，当且仅当这个点前面的斜率都比 $k_0$ 小，它后面的点都比他大。

所以瞪眼法可以得到如果蓝线是 $k_0$ 那么 $D$ 就是决策点。

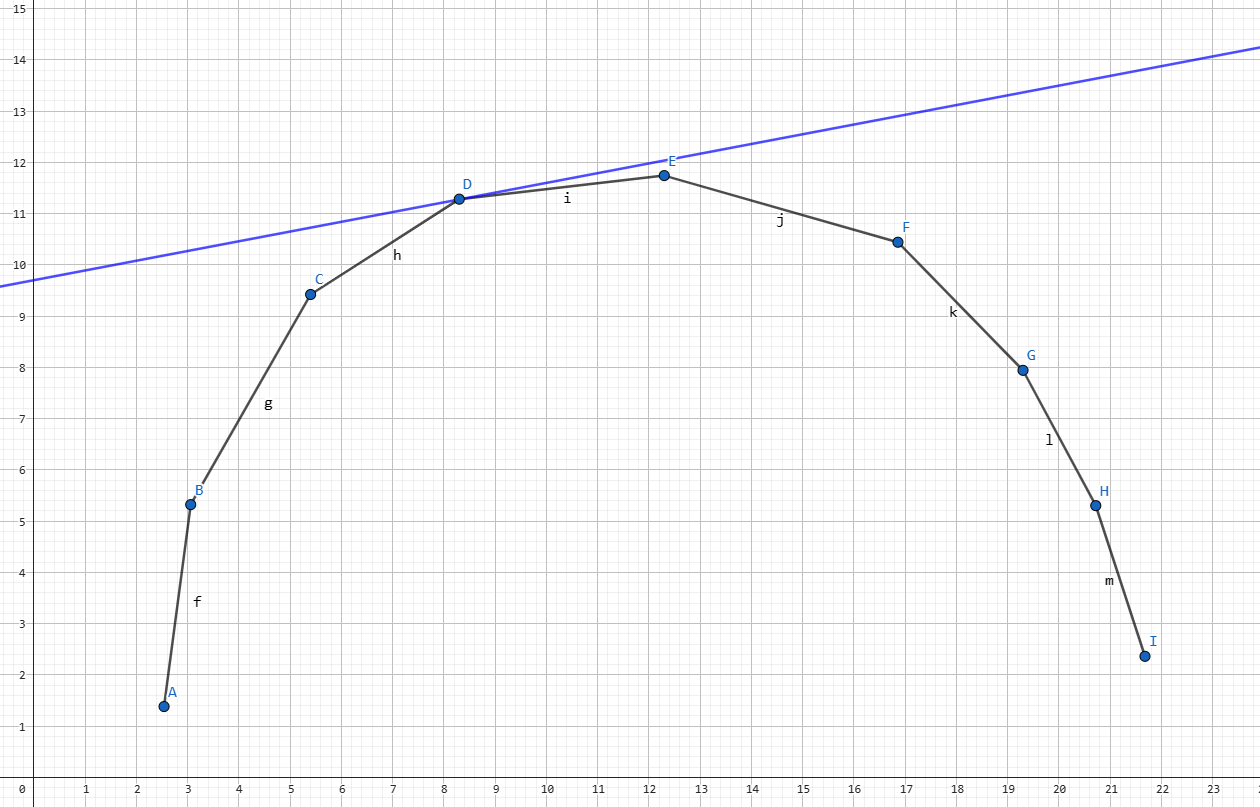
考虑这个东西怎么维护，发现新加入的点的斜率都是 $X$ 坐标都是单调的，那么显然可以直接维护一个可以在末尾添加元素的玩意。

因为上凸包的斜率具有单调性，且寻找的是第一个大于的点，所以可以二分查找，转移的时间复杂度是 $O(\log n)$ 的。

但是发现这个题目的 $k_0$ 也是递增的，所以其实比 $k_0$ 小的以后都不会取到，所以可以直接在末尾弹出元素。

所以最后的时间复杂度为 $O(nk)$，就是一个斜率优化的板子，让某些人复习或者预习一下。

CF1517G Starry Night Camping

将节点的 $x_i,y_i$ 的奇偶性划分成 $A,B,C,D$ 四个集合，注意相邻集合在图中需要时可以满足 $\operatorname{dist}$ 为 $1$ 的。

容易发现对于一个不合法的四边形，一定满足四个帐篷之间的切比雪夫距离均为 $1$ 而且四个点分别属于 $A,B,C,D$ 四个集合。

每一种帐篷只有选择或者不选择，考虑使用最小割进行求解。

因为帐篷 $u$ 无法在最小割中被删除，考虑将 $u$ 拆为两个节点 $u_1,u_2$ 并用权值为 $w_u$ 的边链接 $u_1,u_2$，如果将边 $u_1\to u_2$ 删除，那么就意味着帐篷 $u$ 被放弃掉了。

考虑将集合编号相邻且在图上曼哈顿距离为 $1$ 的节点之间连边，具体的要将编号小的 $x_2$ 向集合编号较大的 $y_1$ 连边边权为 $inf$ 的边。

最后将 $A$ 集合内的所有点与 $S$ 连边，将 $D$ 集合内所有的点与 $T$ 连边，边权都是 $inf$。

显然，如果节点 $a,b,c,d$ 是不合法的帐篷，那么它们显然会被边权为 $inf$ 的边全部连接起来，那么只有割掉任意一条边权不为 $inf$ 的边才可以使 $S,T$ 不连通。根据上面的解释，这也就是放弃了一个帐篷。

时间复杂度为 $O(n^3)$，但是是网络流。

CF1983E I Love Balls

定义一般球被 Alice 拿出的期望次数和平均值分别为 $p_1,s_1$，特殊球为 $p_2,s_2$，那么显然 Alice 拿出的球的期望为 $p_1s_1+p_2s_2$。

因为 Alice 和 Bob 会等概率的拿球，所以 $s_1,s_2$ 就是一般球与特殊球权职和的平均。

考虑没有特殊球的情况，如果将普通球排成一列两个玩家一次取出，显然这样的期望值与题目描述的一样。

但是题目插入了 $k$ 个特殊球，可以理解为将原本的序列分成的几段，每一段只有在最后包含了一个普通球或者不包含，每一个玩家一次取出一段。

发现插入特殊球并没有影响玩家取出普通球的个数，可以得到 $p_1=\lfloor \dfrac{n-k+1}{2}\rfloor$。

显然 Alice 遇到的缝隙的数量是 $\lfloor \dfrac{n-k+2}{2}\rfloor$，每一个缝隙中遇到的球的期望是 $\dfrac{k}{n-k+1}$，所以 $p_2=\dfrac{k\cdot \lfloor \dfrac{n-k+2}{2}\rfloor}{n-k+1}$。

CEOI2017 Building Bridges

设 $s_i=\sum\limits_{j=1}^i w_i$，考虑前 $i$ 个柱子并且保留第 $i$ 个柱子的最小代价。

那么有容易想到朴素的转移方程：

$f_{i}=\min\{f_j+s_{i-1}-s_j+(h_i-h_j)^2\}$

考虑把这个玩意展开，得到：

$f_j+s_{i-1}-s_j+{h_i}^2+{h_j}^2-2\times h_ih_j$

发现出现了乘积项，考虑使用斜率优化。

注意，因为 $w_i$ 有负数所以 $h_i$ 不再递增了。

考虑如果 $h$ 递增，那么下面的分析会假设 $j1<j2$ 以得到 $h_{j1}<h_{j2}$ 来移项，但是实际上我们并没有直接的使用 $j1$ 和 $j2$ 之间的大小关系。

所以我们可以换一种假设方式，假设 $h_{j1}<h_{j2}$ 且 $j2$ 比 $j1$ 优。

套路的可以得到不等式：

$(-2\times h_ih_{j1})+(f_{j1}-s_{j1}+{h_{j1}}^2)+(s_{i-1}+{h_i}^2)>(-2\times h_ih_{j2})+(f_{j2}-s_{j2}+{h_{j2}}^2)+(s_{i-1}+{h_i}^2)$

移项得到：

$2h_i\times (h_{j2}-h_{j1})>(f_{j2}-s_{j2}+{h_{j2}}^2)-(f_{j1}-s_{j1}+{h_{j1}}^2)$

因为有 $h_{j1}<h_{j2}$，所以如果按照 $h$ 排序之后满足下式就可以得到 $j2$ 比 $j1$ 优：

$2h_i>\dfrac{(f_{j2}-s_{j2}+{h_{j2}}^2)-(f_{j1}-s_{j1}+{h_{j1}}^2)}{(h_{j2}-h_{j1})}$

容易发现应该维护下凸壳，考虑让强行让 $h$ 单调。

考虑分治，先处理左区间，然后再用左区间得到的结果处理右区间。

具体的，把左右区间分别递归完之后再归并排序即可，时间复杂度为 $O(n\log n)$。

另外有人发现这是 CDQ 分治吗？

CF1278F Cards 加强

定义 $f_i$ 表示有将 $i$ 个不同的元素组成的特定结构的方案数，$g_i$ 表示从 $i$ 个元素任意选出一些（可以不选）组成特定结构的方案数。

对于知道 $f_i$ 或者 $g_i$ 中的任意一个就可求解另外一个，其公式如下：

$g_n=\sum\limits_{i=0}^n{n\choose i}f_i$

$f_{n}=\sum\limits_{i=0}^n{n\choose i}(-1)^{n-i}g_i$

就是容斥，直接感性理解，相信 ljw 在讲组合数的时候会讲的。

发现有人不会斯特林数，$\begin{Bmatrix}n\\ k\end{Bmatrix}$ 表示把 $n$ 个两两不同的元素，划分为 $k$ 个互不区分的非空子集的方案数。

简单讲一下怎么求通项公式：

设 $G_i$ 表示将 $n$ 个不同元素放入 $i$ 个不同盒子允许为空的方案数，$F_i$ 表示将 $n$ 个不同的元素放入 $i$ 个不同盒子不允许为空的方式。

那么显然：

$G_i=i^n$

同时还有：

$G_i=\sum\limits_{j=0}^i {i\choose j} F_j$

发现上面的式子和二项式反演一样，所以得到：

$F_i=\sum\limits_{j=0}^i (-1)^{i-j}\times {i\choose j}\times G_i$

将 $G$ 带入并化简得到：

$F_i=\sum\limits_{j=0}^i\dfrac{(-1)^{i-j}\times i!\times i^n}{j!\times (i-j)!}$

因为斯特林数的盒子不一样，所以 $F_k$ 就是就是 $\begin{Bmatrix}n\\ k\end{Bmatrix}$ 的 $k!$ 倍，所以得到：

$\begin{Bmatrix}n\\ k\end{Bmatrix}=\dfrac{F_k}{k!}=\sum\limits_{i=0}^k\dfrac{(-1)^{k-i}\times i^n}{i!\times (k-i)!}$

得到：

$i^n=\sum\limits_{j=0}^i j!\times {i\choose j}\times \begin{Bmatrix} n\\j\end{Bmatrix}$

把组合数展开然后约分得到：

$i^n=\sum\limits_{j=1}^i \dfrac{i!}{(i-j)!}\times \begin{Bmatrix} n\\j\end{Bmatrix}$

记抽出王牌的概率 $\dfrac{1}{m}$ 为 $p$，那么按照题目的要求写出式子：

$\sum\limits_{i=0}^n{n\choose i}p^i(1-p)^{n-i}i^k$

把 $i^k$ 根据套路写成第二类斯特林数的形式：

$\sum\limits_{i=0}^n {n\choose i}p^i(1-p)^{n-i}\sum\limits_{k=0}^{j}\begin{Bmatrix}k\\ j\end{Bmatrix}i^{\underline{j}}$

其中 $i^{\underline{j}}$ 表示 $\dfrac{i!}{(i-j)!}$，oi-wiki 里面总计了一些常用的符号。

因为 $n$ 太大了不可以接受，所以考虑把里面的循环提到外面去。

$\sum\limits_{j=0}^k \begin{Bmatrix}k\\ j\end{Bmatrix}\sum\limits_{i=0}^n{n\choose i}i^{\underline{j}}p^i(1-p)^{n-i}$

展开得到：

$\sum\limits_{j=0}^k\begin{Bmatrix}k\\ j\end{Bmatrix}\sum\limits_{i=1}^n\dfrac{i!}{(i-j)!}\dfrac{n!}{i!(n-i)!}p^i(1-p)^{n-i}$

那么合理组合得到：

$\sum\limits_{j=0}^k\begin{Bmatrix}k\\ j\end{Bmatrix}\sum\limits_{i=1}^n\dfrac{(n-j)!}{(i-j)!\times (n-i)!}\times \dfrac{n!}{(n-j)!}\times p^i(1-p)^{n-i}$

考虑组合意义得到：

$\sum\limits_{j=0}^k\begin{Bmatrix}k\\ j\end{Bmatrix}n^{\underline j}\sum\limits_{i=1}^n{n-j\choose i-j}p^i(1-p)^{n-i}$

发现上面的组合数太丑陋了，把 $i-j$ 替换为 $i$ 得到：

$\sum\limits_{j=0}^k\begin{Bmatrix}k\\ j\end{Bmatrix}n^{\underline j}\sum\limits_{i=0}^{n-j}{n-j\choose i}p^{i-j}(1-p)^{n-(i-j)}$

观察式子发现和二项式定理很像：

$(a+b)^n=\sum\limits_{i=0}^n {n\choose i}a^{i}b^{n-i}$

把 $p^i$ 提出来，带入上式得到：

$\sum\limits_{j=0}^k \begin{Bmatrix}k\\ j\end{Bmatrix}n^{\underline j}p^j (p+1-p)^{n-i}$

也就是：

$\sum\limits_{j=0}^k \begin{Bmatrix}k\\ j\end{Bmatrix}\dfrac{n!}{(n-j)!}p^j$

这时可以 $O(k^2)$ 朴素求解斯特林数，也可以只用卷积做到 $O(k\log k)$ 求解，但是还是无法做到线性求解。

把通项公式带入上式：

$\sum_{i=0}^k\dfrac{n^{\underline{i}}p^i}{i!}\sum_{j=0}^i(-1)^{i-j}\binom{i}{j}j^k$

交换求和的顺序：

$\sum_{j=0}^k(-1)^{j}j^k\sum_{i=j}^k\dfrac{n^{\underline{i}}(-p)^i}{i!}\binom{i}{j}$

展开组合数：

$\sum\limits_{j=0}^k(-1)^jj^k\sum\limits_{i=j}^k \dfrac{n^{\underline{i}}(-p)^i}{i!}\times \dfrac{i!}{j!(i-j)!}$

整理一下：

$\sum_{j=0}^k\dfrac{(-1)^{j}j^k}{j!}\sum_{i=j}^k\dfrac{n^{\underline{i}}(-p)^i}{(i-j)!}$

和上面的套路同样的，把 $i$ 替换为 $i+j$ 得到：

$\sum\limits_{j=0}^k\dfrac{(-1)^jj^k}{j!}\sum\limits_{i=0}^{k-j}\dfrac{n^{\underline{i+j}}(-p)^{i+j}}{i!}$

整理一下得到：

$\sum_{j=0}^k\dfrac{(-1)^{j}j^k(-p)^j}{j!}\sum_{i=0}^{k-j}\dfrac{n^{\underline{i+j}}(-p)^i}{i!}$

继续变形得到：

$\sum_{j=0}^k\dfrac{j^kp^jn!}{j!(n-j)!}\sum_{i=0}^{k-j}\dfrac{(n-j)!}{i!(n-i-j)!}\times (-p)^i$

考虑组合意义得到：

$\sum\limits_{j=0}^k\dfrac{j^kp^jn^{\underline j}}{j!}\sum\limits_{i=0}^{k-j}{n-j\choose i}(-p)^i$

观察上式的第二个 $\sigma$ 的前面，发现：

• 阶乘和下降阶乘幂显然可以 $O(k)$ 预处理。
• $g(x)=p^x$ 显然可以 $O(k)$ 预处理。
• $g'(x)=x^k$ 是积性函数，可以通过欧拉筛 $O(k)$ 预处理。

所以我们只需要在 $O(k)$ 或者更低的时间复杂度内求解出后面的玩意就可以了。

考虑设函数：

$f(j)=\sum_{i=0}^{k-j}\binom{n-j}{i}p^i$

那么容易想到可以去递推求解，那么直接考虑两式的差：

$\sum_{i=0}^{k-j+1}\binom{n-j+1}{i}p^i-\sum_{i=0}^{k-j}\binom{n-j}{i}p^i$

那么把可以相像的项写道一起得到：

$\sum_{i=0}^{k-j}p^i\left[\binom{n-j+1}{i}-\binom{n-j}{i}\right]+\binom{n-j+1}{k-j+1}p^{k-j+1}$

因为组合数的意义有：

$\sum_{i=0}^{k-j}p^i\left[{n-j\choose i}+{n-j\choose i-1}-\binom{n-j}{i}\right]+\binom{n-j+1}{k-j+1}p^{k-j+1}$

整理得到：

$\sum_{i=0}^{k-j}\binom{n-j}{i-1}p^i+\binom{n-j+1}{k-j+1}p^{k-j+1}$

同样的处理掉组合数里的 $i-1$ 得到：

$p\sum_{i=0}^{k-j-1}\binom{n-j}{i}p^i+\binom{n-j+1}{k-j+1}p^{k-j+1}$

考虑把 $f(j)$ 带入上式：

$p\left[f(j)-\binom{n-j}{k-j}p^{k-j}\right]+\binom{n-j+1}{k-j+1}p^{k-j+1}$

把式子展开然后提取公因式得到：

$pf(j)+\left[\binom{n-j+1}{k-j+1}-\binom{n-j}{k-j}\right]p^{k-j+1}$

根据组合数的性质，类似与上面的化简得到：

$pf(j)+\binom{n-j}{k-j+1}p^{k-j+1}$

也就是：

$f(j-1)-f(j)=pf(j)+\binom{n-j}{k-j+1}p^{k-j+1}$

消元得到：

$f(j-1)=(p+1)f(j)+\dfrac{n^{\underline{k+1}}}{n^{\underline{j}}(k-j+1)!}p^{k-j+1}$

带入容易得到 $f(\min\{n,k\})=1$，所以原式就是：

$\sum_{j=0}^k\dfrac{j^k(-p)^jn^{\underline{j}}}{j!}f(j)$

注意 $p$ 的符号变了，记得递推的时候处理。

所有操作的时间复杂度均为 $O(k)$，这个问题就解决了。

gym 102331 J Jiry Matchings

做这个题之前需要了解一些前置知识。

定义一个排列是凸序列，当且仅当满足这个序列的差分数组单调不升；反之如果这个序列的差分数组单调不降，那么这个序列就是凹序列。

$\max/\min,+$ 卷积优化 DP，对于这样的一个转移方程：

$f_{i}=\max\limits_{j+k=i} g_j+h_k$

显然这个玩意可以 $O(n^2)$ 的转移，但是如果 $g$ 和 $h$ 都是凸序列，那么就会有更优的做法。

那么把 $f_0$ 初始化为 $g_0+h_0$，然后把两个序列看成：

$\begin{array}{}g_1-g_0,g_2-g_1,g_3-g_2,\cdots,g_{n}-g_{n-1}\\h_1-h_0,h_2-h_1,h_3-h_2,\cdots,h_{n}-h_{n-1}\end{array}$

那么求解 $f_k$ 就相当于在两个序列的开头分别选择一些元素，要求总共选择 $k$ 个元素，然后加上 $f_0$。

因为这两个序列都是上凸的，所以其差分数组是单调不升的，于是贪心的维护两个指针选择最开头的元素中大的那一个就行了，这样也就是可以在 $O(n)$ 的时间复杂度里求解了。

不知道有没有人听说过闵可夫斯基和。

设在以 $x$ 为根的子树中，选择 $i$ 条边且 $x$ 可以被选择得到的匹配的最大值为 $f_{x,i}$。

注意，这里必须是可以选择，否则因为一些神奇的原因 $f$ 不会是一个凸序列。

类似的，设不被选择的最大值为 $g_{x,i}$。

观察发现 $f_x$ 和 $g_x$ 都是凸序列，zjk 都不会证你觉得我会吗。

感性理解一下，树是一个二分图，带权的二分图匹配可以转化成费用流，因为是费用流所以可以通过 zjk 都不会的证明得到是一个凸序列。

显然这样有一个暴力的 DP 转移，在合并的时候是一个类似于背包的转移，仔细观察发现是一个 $\max,+$ 的卷积，刚好可以用凸排列优化，所以我们就可以线性的合并。

但是即使可以线性的合并，但是这样的状态数还是 $O(n^2)$ 的无法通过，使用分治和树剖优化。

考虑减少状态数，即只求解每一个重链的头的 $f$ 和 $g$ 的值。

对于一个重链上的点，先只考虑非重儿子的合并。

考虑递归求解，这样所有的非中儿子的 $f,g$ 都已经求解出来了。

用 FFT 的思想进行分治，每一次把轻儿子分成两半然后合并。

考虑分析时间复杂度，建出递归树，因为每一次区间长度都会减半所以最多只有 $\log n$ 层。

通过 $\max,+$ 卷积合并两个长度为 $o,p$ 的 $f,g$ 的时间复杂度显然为 $O(o+p)$。

假设所有的轻儿子的 $f,g$ 的项数之和为 $m$，那么一层所需的时间复杂度就是 $O(m)$。

因为总共有 $\log n$ 层，所以显然处理轻儿子所需的时间复杂度为 $O(m\log n)$。

通过这个方式合并出轻儿子之后考虑对这个重链上的点进行分治，设 $h_{l,r,0/1,0,1}$ 表示合并了 $[l,r]$ 这个区间，左右端点是否可以选择得到的 $f$ 和 $g$ 的值。

那么同样的如果长度为 $n$，那么用类似上面的分治方法就可以做到 $\log n$ 次合并操作。

因为 $h_{l,r}$ 的项数并不会多于所有的轻儿子的子树的和，所以我们也可以做到 $O(m\log n)$ 的合并。

考虑上面的操作，所有的时间复杂度相加得到最终的时间复杂度为 $O(\sum m\log n)$。

对于树剖，有性质任意一个点到根节点的所经过的重链数量都不会超过 $\log n$。

如果一个节点是重链的开头，那么必然存在一个兄弟节点的大小大于自己，所以这个节点子树的大小至少都会是其父节点的一半。

因为大小每一次都会减半，所以重链最深只会有 $\log n$ 个，自然一个节点向上遍历遇到的重链也不会超过 $\log n$ 条。

对于每一个节点，对于 $\sum m$ 的贡献只会在脱离自己的重链时被计算一次，所以 $(\sum m)=n\log n$，最终的复杂度也就是 $O(n\log^2 n)$。