注意:矩阵树定理支持重边,但不可以存在自环!!!
一些概念
主子式
定义一个有 k 个元素的集合 S 且所有元素都是 [1,n] 中的整数,那么对于任意 i,j∈S 中将行列式 An×n 中的 Ai,j 取出按 (i,j) 的位置放入新的行列式。
最后得到的行列式中,将空缺的区域挤压掉得到的最后的有 k×k 个元素的行列式就称其为矩阵 A 的 k 阶主子式。
举个例子,对于下面的矩阵,如果 S={1,3} 那么变化就是这样的:
⎣⎢⎢⎡15913261014371115481216⎦⎥⎥⎤⇒⎣⎢⎢⎡19311⎦⎥⎥⎤⇒[19311]
余子式
定义一个数 k∈[1,n],那么将行列式的 An×n 的第 k 行和第 k 列删除之后剩余的 (n−1)×(n−1) 的行列式就是 A 的余子式。
举个例子,对于下面的矩阵,如果 k=2 那么变化就是这样的:
⎣⎡147258369⎦⎤⇒⎣⎡1739⎦⎤⇒[1739]
转置矩阵
如果有 i∈[1,n],j∈[1,m],对于矩阵 An×m 和矩阵 Bm×n 满足 Ai,j=Bj,i,那么定义 A=BT。
无向图情况
假设有一个 n 个点的无向图 G,那么定义一下一些矩阵:
-
定义度数矩阵 Dn×n,其意义如下:
Di,j={deg(i)0i=jotherwise
-
定义 #e(i,j) 便是 (i,j) 之间的边的数量。
-
定义边数矩阵 An×n,其定义如下:
Ai,j={#e(i,j)0i=jotherwise
-
定义基尔霍夫矩阵 Ln×n,其定义为 Ln×n=Dn×n−An×n。
-
定义 t(G) 表示无向图 G 的生成树个数。
定理
对于无向图,对于 L 的任意 n−1 阶主子式的值都是相等的,且所有的值都是 t(G)。
证明
引理
引理 1
定义有 m 条边的无向图 G 的 Mn×m 矩阵其意义如下:
Mi,j=⎩⎨⎧−110i is the end of the edgeji is the start of the edgejotherwise
举个例子,对于下图:
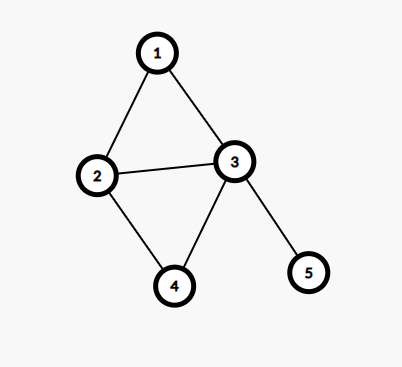
我们将所有的边随意指定一个方向得到:
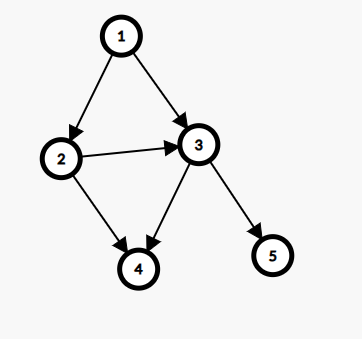
那么 M 矩阵就是下面的样子:
⎣⎢⎢⎢⎢⎡1−100010−10001−100010−10−101000010−1⎦⎥⎥⎥⎥⎤
在一共有的 m 条边中选择出 n−1 条边,如果这个图联通那么这就是一个生成树。将这个操作对应到原来的矩阵 M 就相当于在 m 列中选出 n−1 列构成的 n×(n−1) 的矩阵,我们称之为 M0。
继续举上面的例子,在这个图中随便选择了 n−1 条边之后,就得到了下面的这个图:
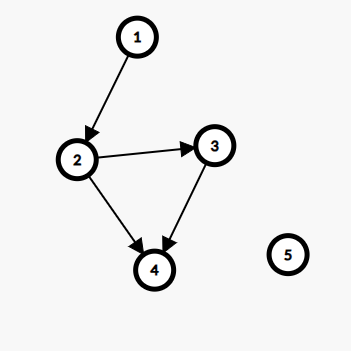
这个图的矩阵 M0 就是下面:
⎣⎢⎢⎢⎢⎡1−100001−100010−10001−10⎦⎥⎥⎥⎥⎤
因为这个矩阵 M0 是 n×(n−1) 的不可以使用行列式求解,所以我们可以将 M0 矩阵删掉一行得到矩阵 M0′。对于所有的选择 n−1条边的方法一共有两个可能性:构成一棵树和不构成一棵树。
对于不构成一棵树的情况必定至少有一个点是与任一点都不连通的,不妨设这个点的编号是 n。那么因为对于每一列的 1 和 −1 都对应这一条边,所以他们出现的数量应该是一样的,所以对于任意的 i∈[1,n−1] 一定有 ∑j=1n−1Mi,j=0。所以将上面的 n−1 行全部相加之后就得到了一个全 0 的一行,所以我们就得到了这个矩阵中的行是线性相关的,那么随意删除一条边是不会影响整个矩阵的。
举个例子,下面的不构成树的矩阵在将前 n−1 行加起来之后就得到了最后一行。
⎣⎢⎢⎢⎢⎡1−100001−100010−10001−10⎦⎥⎥⎥⎥⎤
对于构成一棵树的情况也同理。将这个矩阵所有的行全部相加,因为所有的 1 和 −1 都对应了原图中的一条边也就是他们都是成对出现的。形式化的,对于任意的 i∈[1,n−1] 一定有 ∑j=1nMi,j=0。将前 n−1 行看作一个整体,因为其中的所有元素与第 n 行相加之后都得到了 0,那么所有的元素均互为相反数。所以我们也得到了这个矩阵中的行是线性相关的,那么随意删除一条边必然是不会影响整个矩阵的。
举个例子,将下面的矩阵的前 n−1 行相加就得到了最后一行的每个数都是相反数的一行。
⎣⎢⎢⎢⎢⎡1−100010−100001−100010−1⎦⎥⎥⎥⎥⎤
综上所述,将 M0 转化为 M′ 是不会让元素丢失的。
引理 2
矩阵 M′ 有一个性质:det(M′) 的值在 M′ 不构成树的情况下为 0,反之为 ±1 。
对于不构成树的情况 M′ 中必然存在一个简单环,那么将所有的构成环的行全部相加。如果刚好被删除了也没有关系,因为这是线性相关的,可以构造出来。那么因为在环上的所有点出现的次数都是一样的,所以在将环所包含的所有的点所在的行全部相加会得到两种情况。
如果所有的点都被包含在环中,那么在所有行相加之后一定所有的元素都是 0,所以将前 n−1 行看作一个整体,因为其中的所有元素与第 n 行相加之后都得到了 0,那么所有的元素均互为相反数。所以我们也得到了这个矩阵中的行是线性相关的,所以在高斯消元之后它的对角线会出现一个自由元也就是系数为 0 的情况,那么 det(M′) 显然为 0。
如果不包含所有点的情况,将环中所有包含的点的那些行全部相加。因为这是一个简单环,所以就可以将环所包含的边的那几列全部消成 0,所以容易得到这个矩阵其实也是有自由元的整个矩阵的值为 0。
对于构成树的情况,叶子节点必然满足一行对应行只有一个非零元素。使对应行消去其他行,然后该非零元素对应的行列都只有其一个非零元素。在将全部为 0 的一行与一列删除之后又得到了新的一样的矩阵,在使用归纳法继续递归就可以最终得到只有一个元素且值为 ±1 的矩阵,所以 det(M′) 必然等于 ±1。
引理 3
矩阵 M 还有一个性质:
M×MT=L
根据定义容易得到:
Mi,j×MTi,j=k=1∑mMi,k×MTk,j
根据 MT 的定义得以推得:
Mi,j×MTi,j=k=1∑mMi,k×Mj,k
观察上面的式子容易得到只有 i,j 都是 k 这条边的端点时,Mi,k×Mj,k 才不是 0。
- 对于 i=j 的情况,Mi,k=Mj,k 所以可以写作 Mi,k2 显然无论 Mi,k 的正负答案都是 1,这对应着 degini。
- 对于 i=j 的情况,Mi,k=−Mj,k 因为一条边的两点符号相反,所以 Mi,k×Mj,k=−1,所以贡献肯定为 −1,这对应了 Ai,j。
引理 4(Binet-Cauchy)
定义大小分别为 n×m,m×n(n≤m) 的矩阵 A,B 则有:
det(AB)=S⊆{1,2,⋯m},∣S∣=n∑det(A[S])×det(B[S])
其中 A[S],B[S] 分别表示 A 取 S 集合内的列,B 取 S 集合内的行所构成的矩阵。
首先我们展开等式右侧:
S⊆{1,2,⋯m},∣S∣=n∑det(A[S])×det(B[S])=S⊆{1,2,⋯m},∣S∣=n∑(P∑(−1)λ(P)i=1∏nAi,SPi)×⎝⎛Q∑(−1)λ(Q)i=1∏nBSi,Qi⎠⎞=S∑P∑Q∑(−1)λ(P)+λ(Q)i=1∏nAi,SPi×BSi,Qi
再展开等式左侧:
det(AB)=P∑(−1)λ(P)i=1∏n(j=1∑mAi,j×Bj,Pi)=P∑(−1)λ(P)R∑(i=1∏nAi,Ri×BRi,Pi)(∣R∣=n,∀i,Ri∈{1,2,⋯m})=R∑P∑(−1)λ(P)(i=1∏nAi,Ri)×(i=1∏nBRi,Pi)
仔细观察可知,对于可重排列 R,若存在 i<j,Ri=Rj 那么交换 Pi,Pj 后后面的积式不变,但逆序对奇偶性改变,因此两者贡献互为相反数可抵消。 因此我们只需钦定每个存在 i<j,Ri=Rj 的可重排列 R,让其和交换满足条件的最小 Pi,Pj 交换后的排列 P 的贡献相抵即可。 因为交换最小的 i,j 后依然满足 i,j 为最小的满足条件的点对,因此可以两两唯一配对。 故我们只需枚举不重的序列即可,为此我们首先枚举 {1,2,⋯m} 的子集,然后枚举一个长度为 n 的排列 Q:
det(AB)=S∑Q∑P∑(−1)λ(P)i=1∏nAi,SQi×BSQi,Pi=S∑Q∑PQ′∑(−1)λ(PQ′)(i=1∏nAi,SQi)×(i=1∏nBSi,PQi′)=S∑Q∑PQ′∑(−1)λ(P)+λ(Q)(i=1∏nAi,SQi)×(i=1∏nBSi,PQi′)
整理即可得到从右侧推导得到的式子。
定理证明
记 L 的 n−1 阶主子式为 L0,那么根据引理3可以得到:
det(L0)=det(M′×M′T)
根据引理4可以得到:
det(L0)=S⊆{1,2,⋯,m∧∣S∣=n−1}∑detM′×detM′T
容易发现其中的 S 就是选边的方案,如果合法那么 det2 就是 1 反之即为 0。
显而易见的,这就是生成树的个数。
叶向生成树情况
假设有一个 n 个点的有向图 G,那么定义一下一些矩阵:
-
定义度数矩阵 Dn×n,其意义如下:
Di,j={degin(i)0i=jotherwise
-
定义 #e(i,j) 是 (i→j) 边的数量。
-
定义边数矩阵 An×n,其定义如下:
Ai,j={#e(i,j)0i=jotherwise
-
定义基尔霍夫矩阵 Ln×n,其定义为 Ln×n=Dn×n−An×n。
-
定义 t(G) 表示有向图 G 的叶的生成树个数。
定理
对于无向图,对于 L 的任意 n−1 阶主子式的值都是相等的,且所有的值都是 t(G)。
证明
定义有 m 条边的有向图 G 的 Mn×m 矩阵其意义如下:
Mi,j=⎩⎨⎧−110i is the end of the edgeji is the start of the edgejotherwise
定义矩阵 Dn×m 的意义如下:
Di,j={10ej是vi的入边otherwise
经过观察容易得到 L=M×DT。
根据定义可以得到:
Mi,j×DTi,j=k=1∑mMi,k×DTk,j
根据 DT 的定义可以得到:
Mi,j×DTi,j=k=1∑mMi,k×Dj,k
经过观察可以得到,对于一个 k 这条边只有满足 i,j 都是它的端点才有贡献。
- 对于 i=j 的情况,Mi,k=Dj,k,所以可以写作 Mi,k2 答案显然是 1,这对应着 degini。
- 对于 i=j 的情况,Mi,k=−Dj,k,所以贡献肯定为 −1,这对应了 Ai,j。
对于无向图情况,在求解矩阵 M 是我们人作为指定了方向,所以在有向图情况下,引理1、引理4依旧成立。对于引理2,因为有向图的叶向生成树也满足即使边无向也不存在环,所以引理3也是同样成立的。
所以根据无向图形式的生成树也容易证明,根向生成树的证明也大同小异。
参考资料:



