定义

purfer 序列构造了一组树和序列之间的双射，及确定 prufer 序列可以确定树的形态，知道树的形态可以找到单一的 prufer 序列。

构造方法

1. 每次找到编号最小的叶节点，删掉它并在序列末尾增加它连接到的节点。
2. 重复 $n-2$ 次之后，只剩下两个结点，算法结束。
   注意：这里的树是一棵无根树所以根节点的意义是度为 $1$ 的节点。
   

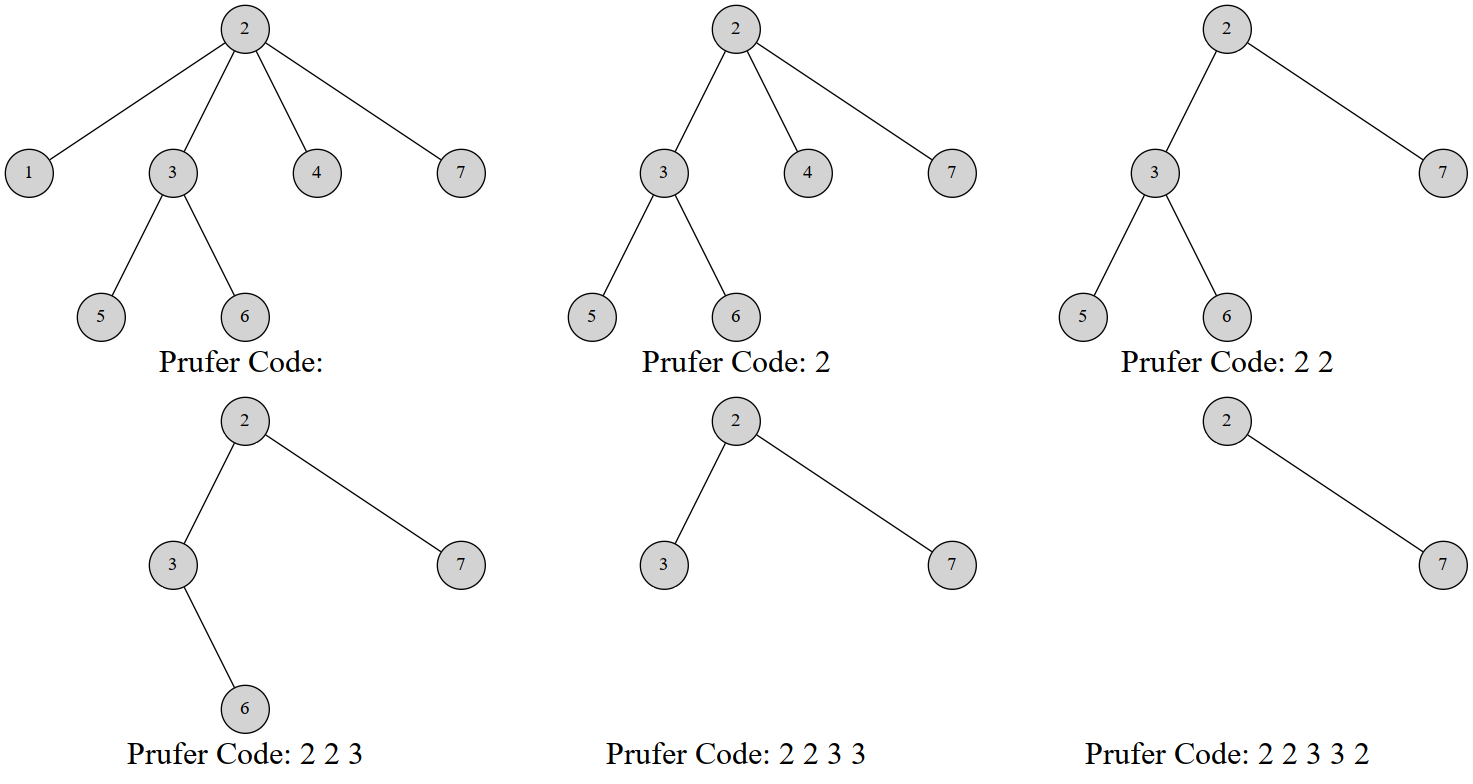
树转化为 prufer

首先需要知道性质：$n$ 号节点在构造 prufer 序列的时候永远都不会被删除。因为这是一棵无根树，那么叶子节点即使在是一条链的情况下也至少有 $2$ 个。无论 $n$ 号节点是否是叶子节点，它都因为编号不是最小的而不会被删除。为了便于实现可以将 $n$ 看为根节点建树，但是注意这是种是以可无根树，这样只是便于实现而已。

对于平凡的做法，使用堆在 $O(n\log n)$ 的时间内求解。

1. 将所有叶子节点放入一个小根堆中。
2. 将堆顶出队，访问其在树上联通的点并更新新节点的度，同时将这个点记录在 purfer 序列中。
3. 如果度为 $1$ 那么将这个节点入队，接着执行操作 $2$ 直到树上的只有 $2$ 个节点没有入队。
4. 执行上述操作知道树内存在的节点不多于 $2$ 个。

对于优雅的方式，其实还有一种线性的算法可以在 $O(n)$ 内求解。因为所有删除的点都是叶子节点，所以每删除一个，新增加的叶子节点定然只有一个。所以我们可以维护一个指针 $p$ 指向最小的叶子节点，进行高效的操作。

1. 删除 $p$ 节点，接着检查新增的叶子节点 $x$。
2. 如果 $x>p$，那么暴力的将 $p$ 向后移动找到新的叶子节点，接着执行操作 $1$。
3. 如果 $x<p$，那么直接删除 $x$ 节点然后反复执行操作 $3$，在不满足条件后进行操作 $2$。
4. 执行上述操作知道树内存在的节点不多于 $2$ 个。

在操作后可以发现 prufer 序列还有一个性质：每一个在节点为序列中出现的次数为它的度 $-1$。首先考虑叶子节点，因为他们的父亲一定不会被删除所以它永远不会出现在 prufer 序列中，满足性质。假设一个点的度不为 $1$，那么在一 $n$ 为根的情况下，它的父亲也永远不会被删去。它的所有的孩子节点都会有这个节点的后代被删除，所以它的所有的儿子节点都会成为叶子节点。而在它的孩子节点被删除的它的度 $-1$ 次后，它也就在 prufer 序列中出现度 $-1$ 次了。

prufer 转化为树

因为 prufer 序列的性质，通过 prufer 序列我们可以得到每一个节点的度。

1. 维护一个指针 $𝑝$，指向当前编号最小的度数等于 $𝟏$ 的结点。
2. 容易得到 $p$ 点一定与当前 prufer 序列的第一个节点连接，那么直接连边即可。
3. 修改连边的两个节点的度，接下来的操作就与树转化为 prufer 一样了。
4. 在 purfer 序列操作结束后将序列中的最后一个数与 $n$ 好节点连边即可。

例题：【模板】Prufer 序列

Link

#include<iostream>
using namespace std;
const int N=5e6+5;
int n,m,fa[N],prufer[N],du[N];
long long ans;
void tree_to_prufer(){
	for(int i=1;i<n;i++){
		cin>>fa[i];
		du[fa[i]]++;
	}
	for(int i=1,p=1;i<=n-2;i++,p++){
		while(du[p]){
			p++;
		}
		prufer[i]=fa[p];
		while(i<=n-2&&!--du[prufer[i]]&&prufer[i]<p){
			prufer[i+1]=fa[prufer[i]];
			i++;
		}
	}
	for(int i=1;i<=n-2;i++){
		ans^=1ll*i*prufer[i];
	}
}
void purfer_to_tree(){
	for(int i=1;i<=n-2;i++){
		cin>>prufer[i];
		du[prufer[i]]++;
	}
	prufer[n-1]=n;
	for(int i=1,p=1;i<n;i++,p++){
		while(du[p]){
			p++;
		}
		fa[p]=prufer[i];
		while(i<n&&!--du[prufer[i]]&&prufer[i]<p){
			fa[prufer[i]]=prufer[i+1];
			i++;
		}
	}
	for(int i=1;i<n;i++){
		ans^=1ll*i*fa[i];
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin>>n>>m;
	if(m==1){
		tree_to_prufer();
	}
	else{
		purfer_to_tree();
	}
	cout<<ans<<'\n';
	return 0;
}