通过向 chatGPT-4o-mini 提问，我注意到所有爬山法可以解决的问题模拟退火都可以解决，所以爬山法死了我不想学爬山法。

具体的，对于一个多峰函数求解最值的题目都可以用模拟退火来做。

如果现在在较优解 $x$，发现了一个新的解 $x'$，如果 $x'$ 比 $x$ 优那么 $x\gets x'$ 否则有一定概率接受 $x'$，这就是模拟退火的核心思想。

考虑 $x'$ 没有 $x$ 优秀的概率是怎么计算的：

令 $\Delta x=x-x'$，那么我们就有 $e^{\frac{\Delta x}{T}}$ 的概率更新 $x$，其中 $T$ 是当前的温度。在进行了一次操作之后就进行降温操作，即 $T\gets T\times 0.999$。

下面的内容很重要！！！！！！

我们令新算出的结果为 $f$，原本的答案为 $lst$。

对于求解最小值的问题，取 $\Delta=f-lst$，那么：

• 如果 $\Delta<0$，那么就直接接受。
• 否则如果 exp(-del/t)>Rand()，那么接受。

对于求解最小值的问题，一样取 $\Delta=f-lst$，那么：

• 如果 $\Delta>0$，那么就直接接受。
• 否则如果 exp(del/t)>Rand()，那么接受。

需要注意的是 exp(x)$=e^x$，其中 $x$ 就是自然函数，其图像如下：

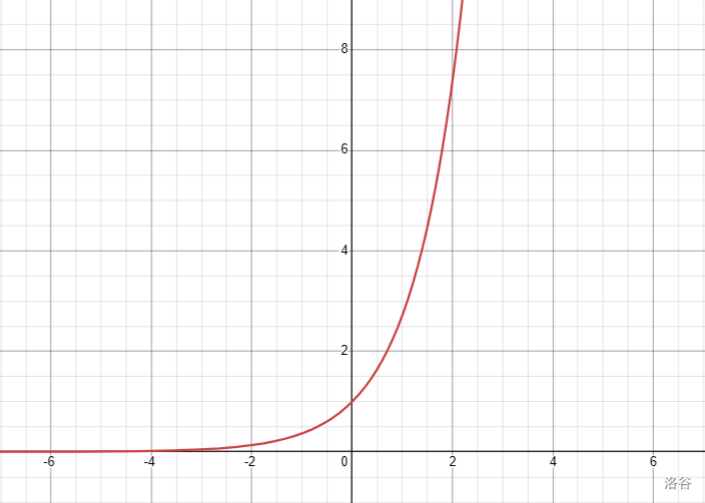
发现对于 $x>0$ 的情况 epx(x) 始终大于 $1$，这个概率就是没有意义的，所以 $\Delta$ 的值一定是负数才有意义。

所以上面的公式在 epx 中是取 del 还是 -del 就十分好理解了，所以这并不需要死记硬背。

形象的，放一张从 OI-Wiki 偷的图：

JSOI2004 平衡点 / 吊打XXX

练手题，但是题目太困难了，考虑给一个形式化题意：

找到一个 $(x,y)$ 使 $\sum\limits_{i=1}^n dis((X_i,Y_i),(x,y))\times Weight_i$ 最小，输出 $x,y$（可以是小数），其中 $1\le n\le 1000$。

就是模板，按照上面的思路写就行了。

AHOI2014/JSOI2014 保龄球

考虑每一次随机交换 $x,y$ 的位置，跑模拟退火就行了。

JSOI2016 炸弹攻击

直接随机放炸弹的位置，因为函数长得奇丑无比所以要求扰动的范围较大，生成的时候需要使用：

double xx=(rand()*2-RAND_MAX)*t+x;

而不是：

double xx=(2.0*rand()/RAND_MAX-1)*t+x;

HAOI2006 均分数据

考虑先随机分组，然后模拟退火随机改变一个元素的分组就行了。

JSOI2008 球形空间产生器

设一个变量 $r$，表示这个高维球体的半径，由公式 $r=\sqrt{\sum_{i=1}^n(a_i-b_i)^2}$ 可得 $\sum_{i=1}^n(a_i-b_i)^2= r^2$，其中 $a_i$ 是高维球面上某一个点的坐标，$b_i$ 是球心的坐标。

化简得：

$\sum_{i=1}^n({a_i}^2-2a_ib_i+{b_i}^2)=r^2$

移项得：

$\sum_{i=1}^n(-2a_ib_i)+\sum_{i=1}^n{b_i}^2-r^2=\sum_{i=1}^n({-a_i}^2)$

其中 $\sum_{i=1}^n{b_i}^2-r^2$ 与球面上的点无关，因此我们可以将其看做一个系数为 $1$ 的变量，右边是常量。