周长

直接按照逆时针或者顺时针围着多边形转动 11 圈，接着统计节点两两之间的距离，最后相加即可。

面积

多边形的面积公式如下：

S=12∑i=1nAPi→×APnex⁡(i)→S=\dfrac{1}{2}\sum_{i=1}^{n}\overrightarrow{AP_i}\times \overrightarrow{AP_{\operatorname{nex}(i)}}

之中 AA 为任意一点，在取原点 (0,0)(0,0) 的情况下面积公式可以化简为：

S=∑i=1nPi→×Pnex⁡(i)→S=\sum_{i=1}^n \overrightarrow{P_i}\times \overrightarrow{P_{\operatorname{nex}(i)}}

通过观察容易发现 12Pi→×Pnex⁡(i)→\dfrac{1}{2}\overrightarrow{P_i}\times \overrightarrow{P_{\operatorname{nex}(i)}} 的几何意义就是一个三角形的有符号面积。

1.PNG

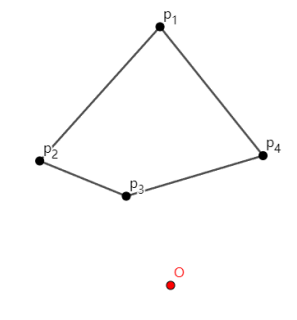
如果需要求解上面的图形面积，那么根据计算公式，计算 12P1→×P2→\dfrac{1}{2}\overrightarrow{P_1}\times \overrightarrow{P_2} 得到：
2.PNG

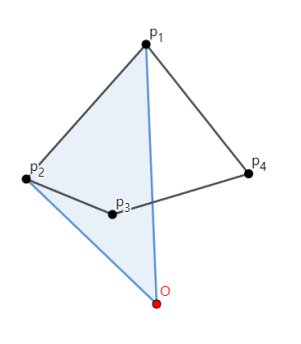
接着计算 12P2→×P3→\dfrac{1}{2}\overrightarrow{P_2}\times \overrightarrow{P_3}，需要注意因为 <P2→,P3→><\overrightarrow{P_2},\overrightarrow{P_3}> 是大于 180°180\degree 所以得到的红色区域是复数的。

3.PNG

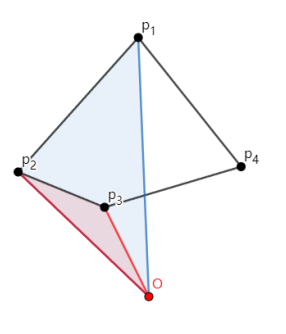
同理，在依次计算剩下的向量之后就可以得到下图：

5.PNG

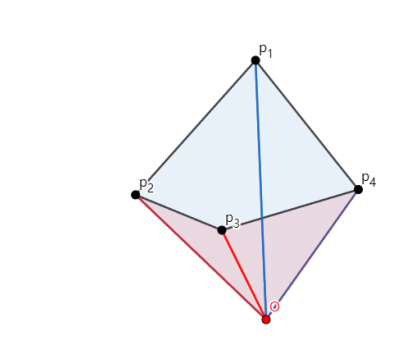
可以看到，所有的查出多边形的蓝色部分已经全部为蓝色部分抵消了，所以就计算出了多边形的面积。

在使用上述公式的情况下，不管可以计算凸多边形的面积，在给整体添加了绝对值之后还可以计算凹多边形的面积。另外可以发现，如果所有的点都是整点，那么 2S2S 一定是一个整数。

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin>>n;
	for(int i=1;i<=n;i++){
		a[i].input();
	}
	db ans=0;
	for(int i=1;i<=n;i++){
		ans+=a[i]%a[i%n+1];
	}
	if(sgn(ans)==-1){
		ans=-ans;
	}
	print(ans/2.0);
	cout<<'\n';
	return 0;
}

判断多边形的凹凸

首先我们不可以直接计算两个向量的夹角，因为我们并不知道我们计算的夹角是位于多边形之内还是多边形外侧。所以我们可以将连续的 33 个点一起考虑，得到这样的两个向量：

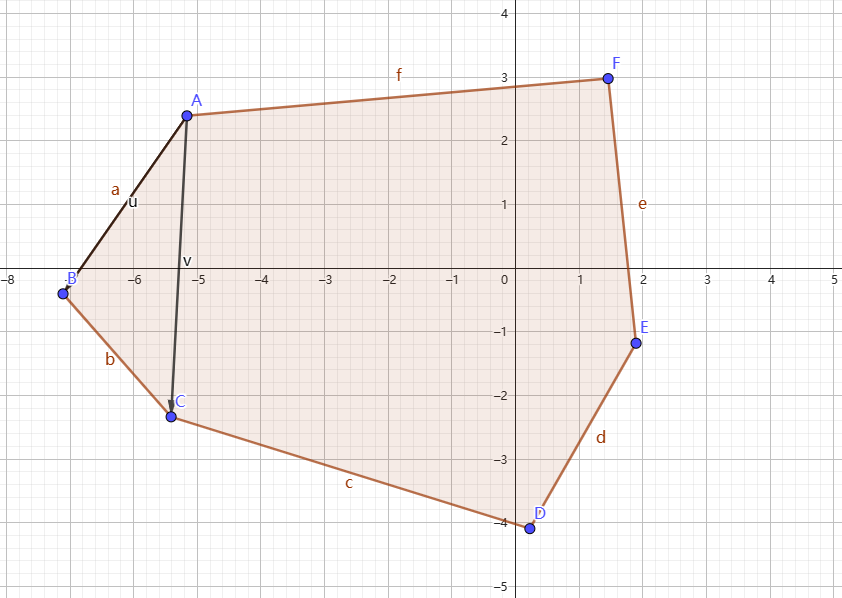
111.PNG

在上图中得到的两个向量是 AB→\overrightarrow{AB} 和 AC→\overrightarrow{AC}，接着计算 AB→×AC→\overrightarrow{AB}\times \overrightarrow{AC} 判断 <AB→,AC→><\overrightarrow{AB},\overrightarrow{AC}> 是否大于 180°180\degree。具体的说，如果 AB→×AC→≥0\overrightarrow{AB}\times \overrightarrow{AC}\ge 0 那么就符合要求了。

对于下面的这个凹多边形会在访问到 DD 点是被判断掉。

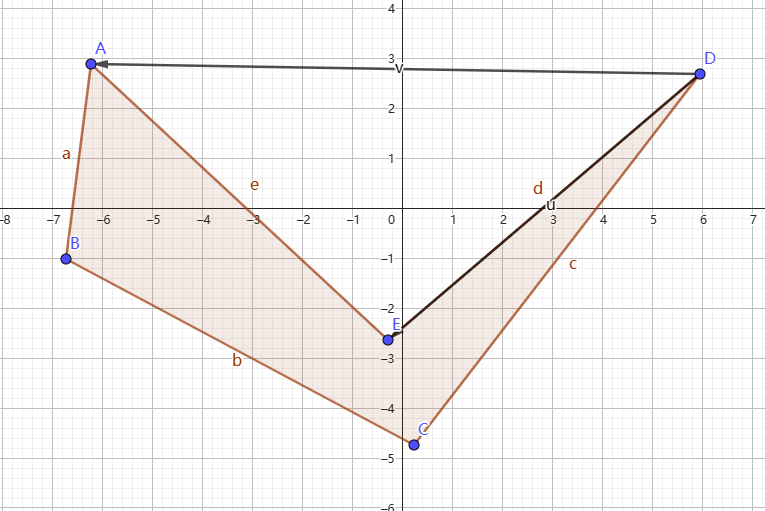
222.PNG

因为 <DE→,DA→><\overrightarrow{DE},\overrightarrow{DA}> 是 DE→\overrightarrow{DE} 逆时针旋转到 DA→\overrightarrow{DA} 大于 180°180\degree，所以 DE→×DA→\overrightarrow{DE}\times \overrightarrow{DA} 是负数也就发现是凹多边形了。

bool solve(){
	for(int i=1;i<=n;i++){
		if(sgn((a[i%n+1]-a[i])%(a[(i+1)%n+1]-a[i]))==-1){
			return 0;
		}
	}
	return 1;
}