点

将点放在直角坐标系中只需要记录一对 (x,y)(x,y) 即可，可以使用结构体进行存储。

struct point{  
    db x,y;
};

向量

对于一个点 PP 也可以视作一个向量 OP→\overrightarrow{OP} ，同样的向量 OP→\overrightarrow{OP} 也可以看作一个点 PP，其中 OO 是坐标为 (0,0)(0,0) 的原点。

根据这种思想，在储存向量时也可以使用 point 进行存储。

辐角

将向量的起点移动到远点之后，从 xx 轴正方向开始逆时针旋转，在和向量重合时所需要的最小叫就是辐角。所以在确定辐角之后，向量的方向也就确定了。

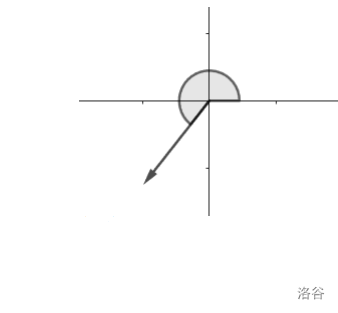
函数 atan2⁡(y,x)\operatorname{atan2}(y,x) 表示直角三角形中，yy 为对边 xx 为临边时夹角的大小。

db phi(){/*夹角*/return atan2(y,x);}

模长

一个向量的起点与重点的欧几里得距离被称为模长，向量 α→\overrightarrow{\alpha} 的模长记作 ∣α∣|\alpha|，欧几里得距离就是 (x1−x2)2+(y1−y2)2\sqrt{(x1-x2)^2+(y1-y2)^2}。

在模长与辐角全部确定之后，向量的所有的信息也就都确定了。

假设辐角为 β\beta，那么有 α→=(∣α∣cos⁡β,∣α∣sin⁡β∣)\overrightarrow{\alpha}=(|\alpha|\cos\beta,|\alpha|\sin\beta|)。

函数 hypot⁡(x,y)\operatorname{hypot}(x,y) 的返回值为 x2+y2\sqrt{x^2+y^2}，可以直接使用此函数求解模长。

db len(){/*模长*/return hypot(x,y);}

加法

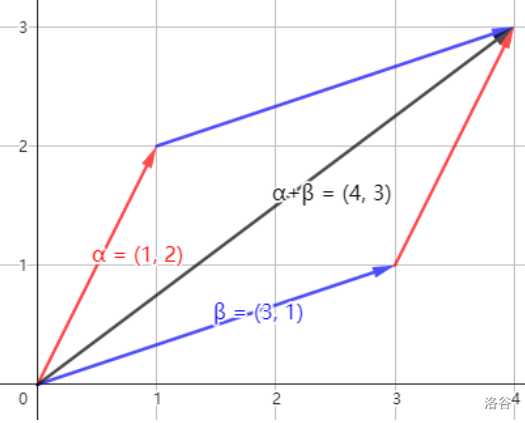
假设 α→=(x1,y1)\overrightarrow{\alpha}=(x_1,y_1)，β→=(x2,y2)\overrightarrow{\beta}=(x_2,y_2)，那么加法操作意义如下：

α→+β→=(x1+x2,y1+y2)\overrightarrow{\alpha}+\overrightarrow{\beta}=(x_1+x_2,y_1+y_2) 

friend point operator + (const point a,const point b){return {a.x+b.x,a.y+b.y};}

减法

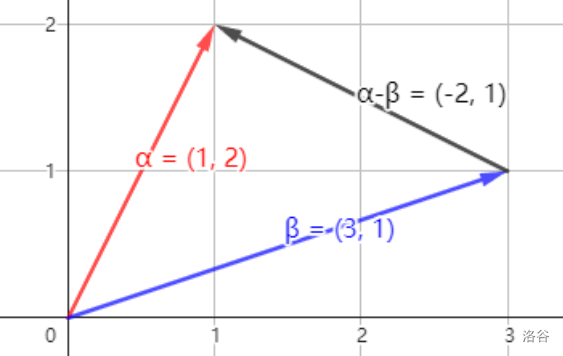
假设 α→=(x1,y1)\overrightarrow{\alpha}=(x_1,y_1)，β→=(x2,y2)\overrightarrow{\beta}=(x_2,y_2)，那么减法操作意义如下：

α→−β→=(x1−x2,y1−y2)\overrightarrow{\alpha}-\overrightarrow{\beta}=(x_1-x_2,y_1-y_2) 

friend point operator - (const point a,const point b){return {a.x-b.x,a.y-b.y};}

系数乘法

假设 α→=(x,y)\overrightarrow{\alpha}=(x,y)，那么系数乘法操作意义如下：

k⋅α→=α→⋅k=(k⋅x,k⋅y)k\cdot \overrightarrow{\alpha}=\overrightarrow{\alpha}\cdot k=(k\cdot x,k\cdot y) 

friend point operator * (const point a,db k){return {a.x*k,a.y*k};}

夹角

夹角具有方向性，<α→,β→><\overrightarrow{\alpha},\overrightarrow{\beta}> 表示 α→\overrightarrow{\alpha} 逆时针旋转到 β→\overrightarrow{\beta} 所需最小的角度。

点乘

假设 α→=(x1,y1)\overrightarrow{\alpha}=(x_1,y_1)，β→=(x2,y2)\overrightarrow{\beta}=(x_2,y_2)，那么点乘操作意义如下：

α→⋅β→=cos⁡<α→,β→>⋅∣α∣⋅∣β∣\overrightarrow{\alpha}\cdot \overrightarrow{\beta}=\cos<\overrightarrow{\alpha},\overrightarrow{\beta}>\cdot |\alpha|\cdot |\beta|

如果乘积小于 00 那么夹角大于 90°90\degree ，如果乘积大于 00 那么夹角小于 90°90\degree，如果乘积等于 00 那么夹角为 90°90\degree。
点乘的几何意义在下图中就是 ∣OB∣⋅∣OC∣|OB|\cdot |OC|。

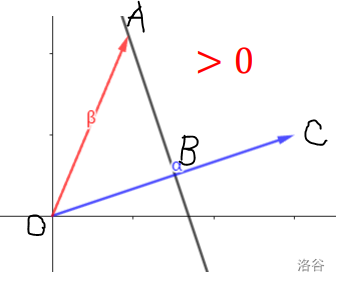
friend db operator ^ (const point a,const point b){return a.x*b.x+a.y*b.y;}

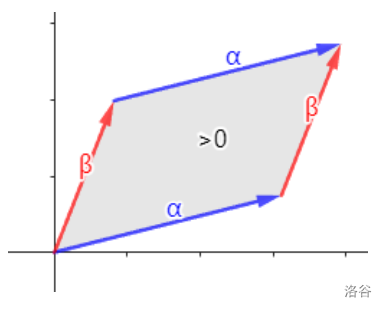
叉乘

假设 α→=(x1,y1)\overrightarrow{\alpha}=(x_1,y_1)，β→=(x2,y2)\overrightarrow{\beta}=(x_2,y_2)，那么叉乘操作意义如下：

α→×β→=sin⁡<α→,β→>⋅∣α∣⋅∣β∣=−β→×α→\overrightarrow{\alpha}\times \overrightarrow{\beta}=\sin<\overrightarrow{\alpha},\overrightarrow{\beta}>\cdot |\alpha|\cdot |\beta|=-\overrightarrow{\beta}\times\overrightarrow{\alpha}

特别的，如果乘积为 00 那么说明两个向量重合。

注意 <α→,β→><\overrightarrow{\alpha},\overrightarrow{\beta}> 是 α→\overrightarrow{\alpha} 逆时针旋转到 β→\overrightarrow{\beta} 所以当这个角度大于 90°90\degree 的时候，sin⁡\sin 的值就是负数。因为 ∣α∣|\alpha| 和 ∣β∣|\beta| 都是整数，所以答案的正负与 sin⁡\sin 是一样的。根据这个性质，当 α→×β→\overrightarrow{\alpha}\times\overrightarrow{\beta} 为负数的时候一定有 <α→,β→><\overrightarrow{\alpha},\overrightarrow{\beta}> 大于 90°90\degree，反之 <α→,β→><\overrightarrow{\alpha},\overrightarrow{\beta}> 就小于 90°90\degree。

friend db operator % (const point a,const point b){return a.x*b.y-a.y*b.x;}

成品