题目大意

就是普通的石子合并，但是添加了限制条件：每一堆石子合并的次数不能超过 $k$ 次。

思路

对于普通的石子合并，将除了最大的石子外的所有的石子全部合并到最大的石子上肯定是最优的。

证明：
假设石子的重量为 $a_1,a_2,a_3,\cdots ,a_{n+1},a_n$，且满足对于 $i\in [1,n-1]$，$a_i\le a_{i+1}$。假设我们要将 $x,y,z$ 三堆石子合并，那么有以下几种可能出现合并的代价：

• $a_x+a_y$，代表将 $x$ 和 $y$ 依次合并到 $z$。
• $a_x+a_z$，代表将 $x$ 和 $z$ 依次合并到 $y$。
• $a_y+a_z$，代表将 $y$ 和 $z$ 依次合并到 $z$。

因为 $a_x\le a_y\le a_z$，所以 $a_x+a_y\le a_x+a_z,a_y+a_z$。可见，在全部依次合并的情况下将除了最大的石子外的所有的石子全部合并到最大的石子上肯定是最优的。
对于现将一堆石子合并到另外一堆再进行合并肯定是更劣的，因为同样的两项的和依然会存在，而且因为一堆被合并了两次，所以还还要多重复一次。

我们可以将这个情况抽象成为一棵树：

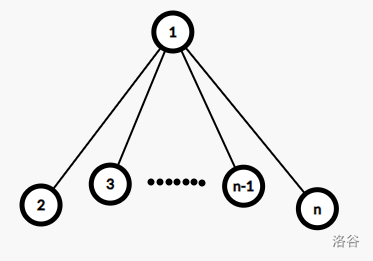
将 $x$ 合并到 $y$ 就相于从 $x$ 到 $y$ 连一条边，这张图的代价为每个点的点权乘以这个点的度 $-1$（即合并次数）的和。因为题目有限制每一堆石子合并的次数不能超过 $k$ 次，所以这个题目求的就是每个节点至多有 $k$ 个孩子的树的代价的最小值。显然，我们可以将 $a$ 数组排序，贪心的从小到大尽可能将每一层都放满。

对于样例首先将输入排序得到 $4,3,2,1,1$。

对于 $k=3$ 时，我们得到了这样的一棵树：

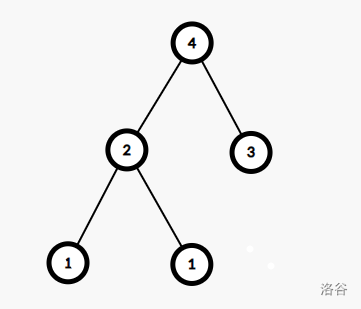
其代价为 $4\times 0+2\times 1+3\times 1+1\times 2+1\times 3=9$。

通过观察可以得到第 $i$ 层有 $k^{i-1}$ 个节点，所以在实际的计算中我们并不需要真正将树建出来，而是直接统计就可以了。

AC Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,a[N],m,k;
map<int,int> mp;
bool cmp(int a,int b){
	return a>b;
}
int ksm(int a,int b){
	int ans=1;
	while(b){
		if(b&1){
			ans=ans*a;
		}
		b>>=1;
		a=a*a;
	}
	return ans;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	sort(a+1,a+1+n,cmp);
	for(int i=1;i<=n;i++){
		a[i]+=a[i-1];
	}
	cin>>m;
	while(m--){
		int ans=0;
		cin>>k;
		if(mp[k]){
			cout<<mp[k]<<' ';
			continue;
		}
		int i=1,cnt;
		for(i=1,cnt=0;i<=n;i+=ksm(k,cnt+1),cnt++){
			ans+=(a[i]-a[i-ksm(k,cnt)])*cnt;
		}
		i-=ksm(k,cnt);
		ans+=(a[n]-a[i])*(cnt);
		mp[k]=ans;
		cout<<ans<<' ';
	}
	return 0;
}