CF1204E Natasha, Sasha and the Prefix Sums
考虑设 为前缀最大值比 大的数量,那么显然答案就是 。
考虑将选择 转化为 的位移,所以根据题目要求从 出发必须以 作为终点。
比如下图就对应了 这个序列:
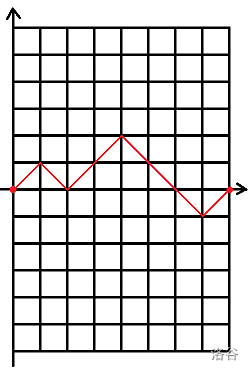
那么如果一个路径想要给 贡献答案,那么就一定需要经过 这个常值函数函数才可以。
如果如果 也就是起点与终点的函数的异侧就一定会相交,所以 。
如果 ,那么就把起点从 翻转到 就与上一种情况一样了,所以 。
放一张图辅助理解:
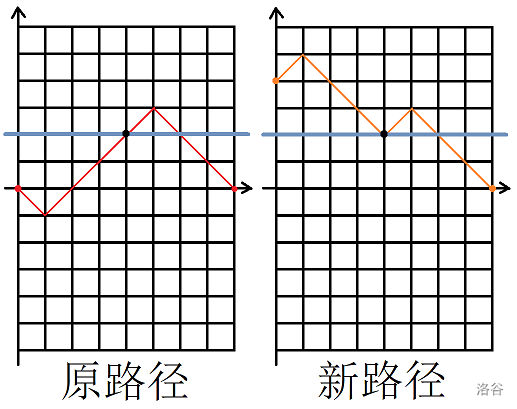

考虑设 为前缀最大值比 大的数量,那么显然答案就是 。
考虑将选择 转化为 的位移,所以根据题目要求从 出发必须以 作为终点。
比如下图就对应了 这个序列:

那么如果一个路径想要给 贡献答案,那么就一定需要经过 这个常值函数函数才可以。
如果如果 也就是起点与终点的函数的异侧就一定会相交,所以 。
如果 ,那么就把起点从 翻转到 就与上一种情况一样了,所以 。
放一张图辅助理解:

