定义

对于欧拉回路满足回路数量 $cnt$ 满足：

$cnt=T\prod_{i=1}^{n}(out_i-1)!$

其中 $T$ 为图中一任一点为根的外向生成树（根据欧拉图的性质所有的节点作为根的结果都是一样的），$out_i$ 表示 $i$ 点的出度。

显然，$T$ 可以使用矩阵树定理进行求解。

证明

令 $s$ 为根，如果一个图为以 $s$ 点为根的内向生成树那么满足一共有 $n-1$ 条有向边期且对于任一点都可以找到一条路径到 $s$。

对于任意一条欧拉路，将所有的点在遍历时访问到的最后一条出边删掉，剩下的图一定成为一棵以 $s$ 为根的内向生成树。

例如下面这张图：

假设路径为 $s\to 1\to 2\to 3\to 4\to 5\to s\to 2\to 4\to s$，那么经过处理图就成为了这样：

经过整理之后就得到了一个以 $s$ 为根的内向生成树：

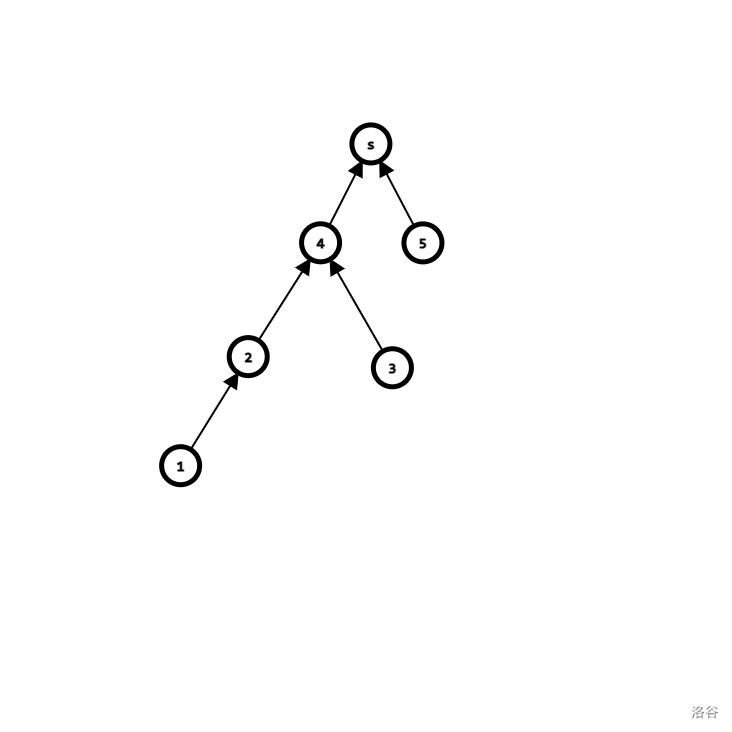
因为所有的点均保留了自己的最后一条出边而且所有的节点在最后全部到达了 $s$ 点，那么所有的点一定有一个路径可以到达 $s$ 点。假设成为了环，那么交点处因为入度等于出度，一定还会有一条出边，所以形成环与条件相矛盾。

从起点 $s$ 出发最终回到 $s$ 点一共 $out_s$ 次就一共有 $out_s!$ 种可能性。因为剩下的所有点都有 $out_i-1$ 条没有被固定的出边，所有都有 $(out_i-1)!$ 种方案。因为乘法原理，所以将它们乘起来即可。

由于所有点的保留的出边中一定有欧拉回路顺序中的最后一条边，所以通过这条边一定可以回到 $s$，得到了这种构造方式的正确性。

但考虑从任意一条边开始，那么在上面的方法中我们将所有的路径以 $s$ 划分成了 $out_s$ 段。但是因为不在存在起点，所以这且路径本质上是相同的，那么答案就应该除以 $out_s$。

实现

需要注意 Best 定理只能在欧拉图上使用，所以在每一次使用前都应该判断输入的是否是欧拉图。

因为可能有一些节点是独立的不与任何节点有连边，那么这个节点就是不需要考虑的，需要在实现中特判掉。

根据定理求出的数量时间复杂度为 $O(T\cdot n^2\log W)$ 其中 $W$ 为值域。

Code

#include<iostream>
#include<vector>
#include<cstring>
#define int long long
using namespace std;
const int N=105,M=2e5+5,mod=1e6+3;
int n,m,in[N],out[N],a[N][N],jc[M],cnt;
bool vis[N];
vector<int> v[N];
void dfs(int x){
	for(int i:v[x]){
		cnt++;
		if(!vis[i]){
			vis[i]=1;
			dfs(i);
		}
	}
}
bool ck(){
	vis[1]=1,cnt=0,dfs(1);
	if(m!=cnt){
		return 0;
	}
	for(int i=1;i<=n;i++){
		if(out[i]!=in[i]){
			return 0;
		}
	}
	return 1;
}
int get(){
	int ans=1;
	for(int i=2;i<=n;i++){
		if(!vis[i]) continue;
		for(int j=i+1;j<=n;j++){
			if(!vis[j]) continue;
			while(a[j][i]){
				int tot=a[i][i]/a[j][i];
				for(int k=1;k<=n;k++){
					a[i][k]=(a[i][k]-a[j][k]*tot%mod+mod)%mod;
				}
				swap(a[i],a[j]);
				ans*=-1;
			}
		}
	}
	for(int i=2;i<=n;i++){
		if(vis[i]) ans=(ans*a[i][i]%mod+mod)%mod;
	}
	return ans;
}
void solve(){
	cin>>n,m=0;
	memset(in,0,sizeof(in));
	memset(vis,0,sizeof(vis));
	memset(a,0,sizeof(a));
	for(int i=1;i<=n;i++) v[i].clear();
	for(int i=1;i<=n;i++){
		cin>>out[i];
		for(int j=1,x;j<=out[i];j++){
			cin>>x;
			v[i].push_back(x);
			in[x]++;
			a[i][i]++;
			a[i][x]--;
			m++;
		}
	}
	if(!ck()){
		cout<<0<<'\n';
		return;
	}
	int ans=get()*jc[out[1]]%mod;
	for(int i=2;i<=n;i++){
		if(!vis[i]){
			continue;
		}
		ans=ans*jc[out[i]-1]%mod;
	}
	cout<<ans<<'\n';
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int T;cin>>T;
	jc[0]=1;
	for(int i=1;i<M;i++){
		jc[i]=jc[i-1]*i%mod;
	}
	while(T--){
		solve();
	}
	return 0;
}