注意到 $x$ 可以与 $\lfloor\dfrac{x}{2}\rfloor$ 交换，即 $k,2k,2k+1$ 之间可以交换，容易联想到完全二叉树。

假设位置 $k,2k,2k+1$ 的值分别是 $A,B,C$，考虑分类讨论。

对于 $A$ 最小的情况，显然不应该交换。因为字典序可以贪心的选择，如果 $k$ 的位置比 $A$ 大，那么在前面都一样的情况下，显然直接取 $A$ 是最优的。

对于 $B$ 最小的情况，显然应该让 $k,2k$ 交换，原因与上面类似。

对于 $C$ 最小的情况，应该让让 $k,2k+1$ 交换。但是特殊的情况是无论是否交换 $k,2k$ 都可以使 $k$ 这个位置取到最小的 $C$。假设 $A$ 为次小值，需要注意将 $A$ 放到 $2k$ 的位置并不是最优，下图就是一个反例。

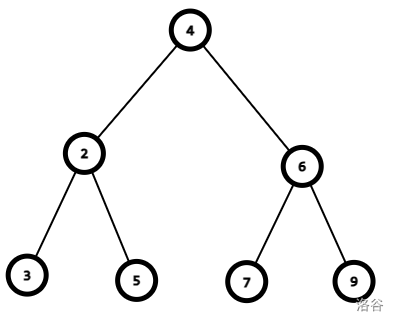
对于这样的树形结构

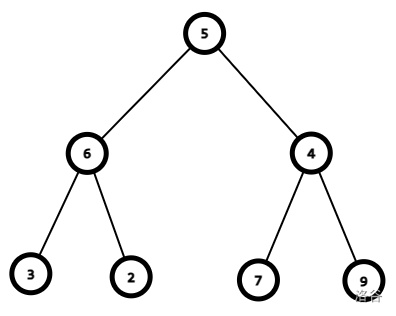
应该进行这样的变换：

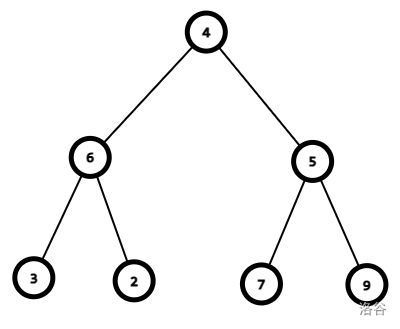
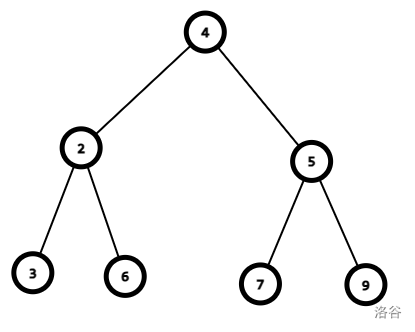
而不是如上述的贪心策略进行这样的变化：

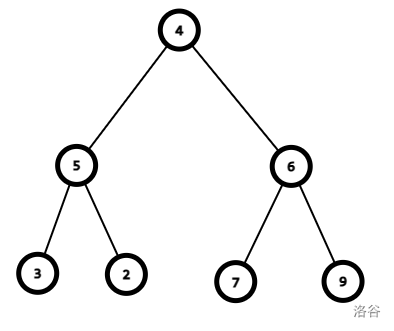
考虑设 $f(x,v)$ 为 $x$ 这个位置在处理了 $\lfloor \dfrac{x}{2}\rfloor$ 之后为 $v$ 时，$v$ 这个值可以移动到的最小位置。

对于上面的情况，我们就只需要考虑 $f(2k,a),f(2k+1,a)$ 的大小关系，$a$ 就应该换到小的那个子树。

考虑证明这个决策的正确性，不妨设放到 $2k$ 得到的序列为 $x$，反之为 $y$，且 $f(2k,a)\lt f(2k+1,a)$。

要证决策正确性，只需要证明 $\forall i\in[1,\min(f(2k,a),f(2k+1,a)))\cap\mathbb{N}$ 满足 $x_i=y_i$ 且 $x_{f(2k,a)}\lt y_{f(2k,a)}$。

要证明 $\forall i\in[1,\min(f(2k,a),f(2k+1,a)))\cap\mathbb{N}$ 满足 $x_i=y_i$，只需证 $\forall i\in[1,k]\cup(k,\min(f(2k,a),f(2k+1,a))))\cap\mathbb{N}$ 满足 $x_i=y_i$。

因为 $\forall i\in[1,k]\cap\mathbb{N}$ 的选择已经完成，那么显然都有 $x_i=y_i$。

因为 $a$ 这个值可以一直移动到 $f(2k,a)$，说明在在从 $2k$ 向下一直转移到 $f(2k,a)$ 都没有遇到取 $a$ 是最优的情况。那么如果 $2k$ 这个位置放比 $a$ 还要劣的 $b$，在从 $2k$ 向下遍历的时候遇到取 $b$ 是最优的一定不早于 $f(2k,a)$ ，对于在 $2k+1$ 的子树也是一样的。

这就证明了 $\forall i\in[1,\min(f(2k,a),f(2k+1,a)))\cap\mathbb{N}$ 满足 $x_i=y_i$。

根据定义因为 $a$ 会放到 $f(x,a)$，那么 $2\times f(x,a),2\times f(x,a)+1$ 都没有 $a$ 优秀，所以无论这个位置取 $b$ 还是 $2\times f(x,a),2\times f(x,a)+1$ 对应的值都没有 $a$ 优秀，因此策略的正确性得证。

考虑通过深度优先搜索求解 $f(x,v)$。

如果遇到第 $1$ 种情况或者遇到了根节点，那么显然就可以直接回溯求出答案，因为此时位置已经确定。

如果遇到第 $2$ 种情况，那么显然应该继续进入左子树进行递归。

对于第 $3$ 种情况就模仿现在的情况进行递归两个儿子就可以了。

#include<iostream>
#include<map>
#include<algorithm>
#define ls k*2
#define rs k*2+1
using namespace std;
const int N=4e5+5;
map<int,int> f[N];
int a[N],n;
int solve(int k,int s){
    if(f[k].count(s)){
        return f[k][s];
    }
    int ans=0;
    if(!a[ls]){
        return f[k][s]=k;
    }
    if(!a[rs]){
        if(a[ls]<s){
            return f[k][s]=ls;
        }
        return f[k][s]=k;
    }
    int A=s,B=a[ls],C=a[rs],v=min({A,B,C});
    if(A==v){
        return f[k][s]=k;
    }
    if(B==v){
        return f[k][s]=solve(ls,s);
    }
    int x=solve(ls,min(A,B)),y=solve(rs,min(A,B));
    if(s==min(A,B)){
        return f[k][s]=min(x,y);
    }
    if(x<y){
        return f[k][s]=solve(rs,s);
    }
    return f[k][s]=solve(ls,s);
}

void dfs(int k){
    if(k>n) return;
    int A=a[k],B=a[ls],C=a[rs],v=min({A,B,C});
    if(!B){
        return;
    }
    if(!C){
        if(B<A){
            swap(a[ls],a[k]);
        }
        return;
    }
    if(A==v){
        dfs(ls),dfs(rs);
        return ;
    }
    if(B==v){
        swap(a[k],a[ls]);
        dfs(ls),dfs(rs);
        return ;
    }
    a[k]=C;
    int x=solve(ls,min(A,B)),y=solve(rs,min(A,B));
    a[ls]=min(A,B),a[rs]=max(A,B);
    if(y<x){
        swap(a[ls],a[rs]);
    }
    dfs(ls),dfs(rs);
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    dfs(1);
    for(int i=1;i<=n;i++){
        cout<<a[i]<<' ';
    }
    return 0;
}