题目大意

有 $n$ 卡片在桌子上，每张卡牌正反两面分别有一个颜色。第 $i$ 牌的正面的颜色为 $a_i$
，背面为 $b_i$。
对于每张牌，可以选择正面或者背面朝上。所有可能的情况中出现的不同的颜色的数量的最大值。

思路

考虑建图，将 $a_i$ 与 $b_i$ 连边。如果一个联通块内有环则整个联通块都可以选择，否则有 $1$ 个点将被舍弃。

因为如果出现环的情况，换上的所有点都可以通过自己一侧的边被选择，而因为环上的点全部都自给自足了，所有从环外连到环内的点都可以由向环内连接的那条进行选择。

具体来说，假设一个联通块如图所示：

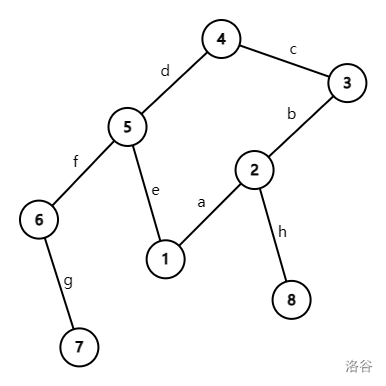
那么 $1,2,3,4,5$ 号在环上的节点均可以通过环上的边 $\texttt{a},\texttt{b},\texttt{c},\texttt{d},\texttt{e}$ 进行选择。

而因为这些环上的节点均已经通过环上的边进行选择，那么 $6,7,8$ 号节点就可以通过他们向环的方向连的边 $\texttt{f},\texttt{g},\texttt{h}$ 进行选择。

对于不存在环的情况，如下图：

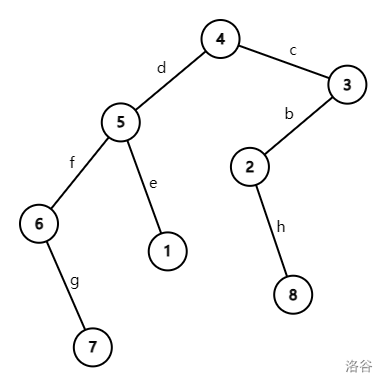
$8,2,3,4,5,6,7$ 号节点均可以通过 $\texttt{h},\texttt{b},\texttt{c},\texttt{e},\texttt{f},\texttt{g},$ 进行选择。

而 $1$ 号节点则无边可用，自然就被舍弃了。

AC Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=4e5+6;
int n,m,ans,cnt,flag;
bool vis[N];
vector<int> v[N];
void dfs(int x,int fa){
	cnt++;
	for(int i:v[x]){
		if(i!=fa&&vis[i]){
			flag=0;
		}
		if(!vis[i]){
			vis[i]=1;
			dfs(i,x);
		}
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin>>m;
	for(int i=1,x,y;i<=m;i++){
		cin>>x>>y;
		v[x].push_back(y);
		v[y].push_back(x);
		n=max({n,x,y});
	}
	for(int i=1;i<=n;i++){
		if(!vis[i]){
			vis[i]=1;
			flag=1,cnt=0;
			dfs(i,0);
			ans+=cnt-flag;
		}
	}
	cout<<ans<<'\n';
	return 0;
}